2017年山东省济宁市微山县中考数学模拟试卷（2月份）

试卷更新日期：2017-04-24 类型：中考模拟

进入出卷网下载

一、选择题

1. $\sqrt{16}$ 的平方根是（）

A、4 B、±4 C、2 D、±2

查看试题解析
2. 从长度分别为2、3、4、5的4条线段中任取3条，能构成钝角三角形的概率为（　　）

A、 $\frac{3}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
3. H7N9型禽流感是一种新型禽流感，于2013年3月底在上海和安徽两地率先发现．H7N9型禽流感是全球首次发现的新亚型流感病毒，其细胞的直径约为0.000000106m，用科学记数法表示这个数是（）

A、0.106×10^﹣⁶m B、0.106×10⁶m C、1.06×10^﹣⁷m D、1.06×10⁷m

查看试题解析
4. 如果用□表示1个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么下面图是由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（）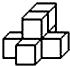

A、 B、 C、 D、

查看试题解析
5. 一条开口向下的抛物线的顶点坐标是（2，3），则这条抛物线有（）

A、最大值3 B、最小值3 C、最大值2 D、最小值﹣2

查看试题解析
6. 如图，直径为10的⊙A经过点C（0，5）和点O（0，0），B是y轴右侧⊙A优弧上一点，则∠OBC的余弦值为（）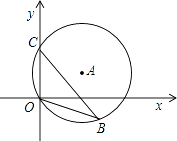

A、 $\frac{1}{2}$ B、 $\frac{3}{4}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{5}{4}$

查看试题解析
7. 如图，梯形ABCD的对角线AC、BD相交于O，G是BD的中点．若AD=3，BC=9，则GO：BG=（）

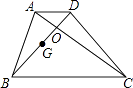A、1：2 B、1：3 C、2：3 D、11：20

查看试题解析
8. 在下列命题中，正确的是（）

A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
9. 如图，已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m （am+b）（m≠1的实数）．其中正确结论的有（）

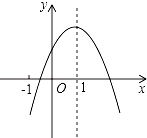A、①②③ B、①③④ C、③④⑤ D、②③⑤

查看试题解析
10. 已知点A（﹣2，1），B（1，4），若反比例函数y= $\frac{k}{x}$ 与线段AB有公共点时，k的取值范围是（）

A、﹣2≤k≤4 B、k≤﹣2或k≥4 C、﹣2≤k＜0或k≥4 D、﹣2≤k＜0或0＜k≤4

查看试题解析

二、填空题

11. 如果代数式 $\frac{\sqrt{x + 1}}{x - 2}$ 有意义，那么字母x的取值范围是

查看试题解析
12. 已知a+b=3，ab=﹣2，则a²+b²的值是．

查看试题解析
13. 随着新农村建设的进一步加快，农村居民人均纯收入增长迅速．据统计，某市农村居民人均纯收入由2012年的14000元增长到2014年的16940元，则这个市从2012年到2014年的年平均增长的百分率是．

查看试题解析
14. 如图平行四边形ABCD中，∠ABD=30°，AB=4，AE⊥BD，CF⊥BD，且，E，F恰好是BD的三等分点，又M、N分别是AB，CD的中点，那么四边形MENF的面积是．

查看试题解析
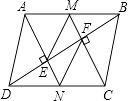15. 如图，四边形ABCD与EFGH均为正方形，点B、F在函数y= $\frac{1}{x}$ （x＞0）的图象上，点G、C在函数y=﹣ $\frac{3}{x}$ （x＜0）的图象上，点A、D在x轴上，点H、E在线段BC上，则点G的纵坐标．

查看试题解析
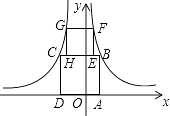16. 如图，等腰直角三角形OAB的一条直角边在y轴上，点P是边AB上的一个动点，过点P的反比例函数y= $\frac{k}{x}$ 的图象交斜边OB于点Q，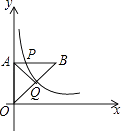

(1)、当Q为OB中点时，AP：PB=

(2)、若P为AB的三等分点，当△AOQ的面积为 $\sqrt{3}$ 时，k的值为

查看试题解析

三、解答题

17. 计算： $\sqrt{27}$ ﹣（﹣ $\frac{1}{3}$ ）^﹣¹+（﹣ $\sqrt{2}$ ）⁰﹣6sin60°．

查看试题解析
18. 解方程：1﹣ $\frac{x}{x + 1}$ = $\frac{2 x + 3}{x^{2} - 1}$ ．

查看试题解析
19. 如图，AC是圆O的直径，AB、AD是圆O的弦，且AB=AD，连结BC、DC．

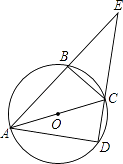(1)、求证：△ABC≌△ADC；

(2)、延长AB、DC交于点E，若EC=5cm，BC=3cm，求四边形ABCD的面积．

查看试题解析
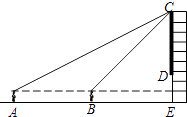
20.
如图所示，小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕，测得屏幕上端C处的仰角为30°，接着他正对电子屏幕方向前进7m到达B处，又测得该屏幕上端C处的仰角为45°．已知电子屏幕的下端离开地面距离DE为4m，小杨的眼睛离地面1.60m，电子屏幕的上端与墙体的顶端平齐．求电子屏幕上端与下端之间的距离CD（结果保留根号）．

查看试题解析
21. 已知如图，△ABC是等边三角形，过AB边上的点D作DG∥BC，交AC于点G，在GD的延长线上取点E，使DE=CG，连接AE、CD．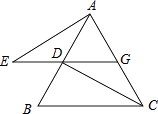

(1)、求证：△AGE≌△DAC；

(2)、过E做EF∥DC．交BC于F．连接AF．判断△AEF是怎样的三角形．并证明你的结论．

查看试题解析
22. 某公司生产一种新型节能电水壶并加以销售，现准备在甲城市和乙城市两个不同地方按不同销售方案进行销售，以便开拓市场．
若只在甲城市销售，销售价格为y（元/件）、月销量为x（件），y是x的一次函数，如表，
月销量x（件）
1500
2000
销售价格y（元/件）
185
180
成本为50元/件，无论销售多少，每月还需支出广告费72500元，设月利润为W_甲（元）
（利润=销售额﹣成本﹣广告费）．
若只在乙城市销售，销售价格为200元/件，受各种不确定因素影响，成本为a元/件（a为常数，40≤a≤70），当月销量为x（件）时，每月还需缴纳 $\frac{1}{100}$ x²元的附加费，设月利润为W_乙（元）（利润=销售额﹣成本﹣附加费）．

(1)、当x=1000时，y_甲=元/件，w_甲=元；

(2)、分别求出W_甲， W_乙与x间的函数关系式（不必写x的取值范围）；

(3)、当x为何值时，在甲城市销售的月利润最大？若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同，求a的值；

(4)、如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在甲城市还是在乙城市销售才能使所获月利润较大？

查看试题解析
23.
已知：如图，在平面直角坐标系xOy中，直线y= $\frac{3}{4}$ x+6与x轴、y轴的交点分别为A、B两点，将∠OBA对折，使点O的对应点H落在直线AB上，折痕交x轴于点C．

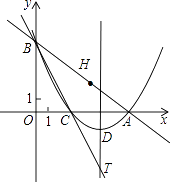(1)、直接写出点C的坐标，并求过A、B、C三点的抛物线的解析式；

(2)、若（1）中抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由；

(3)、若把（1）中的抛物线向左平移3.5个单位，则图象与x轴交于F、N（点F在点N的左侧）两点，交y轴于E点，则在此抛物线的对称轴上是否存在一点Q，使点Q到E、N两点的距离之差最大？若存在，请求出点Q的坐标；若不存在，请说明理由．

查看试题解析

月销量x（件）	1500	2000
销售价格y（元/件）	185	180