2017年河南省许昌市禹州市中考数学一模试卷
试卷更新日期:2017-04-24 类型:中考模拟
一、选择题
-
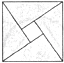
1. 实数﹣π,﹣3.14,0, 四个数中,最小的是( )A、﹣π B、﹣3.14 C、 D、02. 下列运算正确的是( )A、﹣(﹣a+b)=a+b B、3a3﹣3a2=a C、(x6)2=x8 D、1÷( )﹣1=3. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、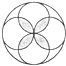 C、
C、 D、
D、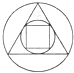 4. 小明因流感在医院观察,要掌握他在一周内的体温是否稳定,则医生需了解小明7天体温的( )A、众数 B、方差 C、平均数 D、频数5. 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
4. 小明因流感在医院观察,要掌握他在一周内的体温是否稳定,则医生需了解小明7天体温的( )A、众数 B、方差 C、平均数 D、频数5. 如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( ) A、80° B、90° C、100° D、102°6. 已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′于点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为( )A、(3,0) B、(3,﹣3) C、(3,﹣1) D、(﹣1,3)7. 几个棱长为1的正方体组成的几何体的三视图如图所示,则这个几何体的体积是( )
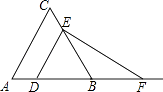
A、80° B、90° C、100° D、102°6. 已知点A(﹣1,0)和点B(1,2),将线段AB平移至A′B′,点A′于点A对应,若点A′的坐标为(1,﹣3),则点B′的坐标为( )A、(3,0) B、(3,﹣3) C、(3,﹣1) D、(﹣1,3)7. 几个棱长为1的正方体组成的几何体的三视图如图所示,则这个几何体的体积是( ) A、4 B、5 C、6 D、78.
A、4 B、5 C、6 D、78.如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 分解因式:a3﹣4a2b+4ab2= .10. 南海是我国固有领海,南海面积超过东海、黄海、渤海面积的总和,约为360万平方千米.360万平方千米用科学记数法可表示为平方千米.11. 如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为 .
 12. 在一个不透明的口袋中装有若干只有颜色不同的球,如果口袋中装有3个红球,且摸出红球的概率为 ,那么袋中共有个球.13. 不等式组 的解集为 .14. 如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为°.
12. 在一个不透明的口袋中装有若干只有颜色不同的球,如果口袋中装有3个红球,且摸出红球的概率为 ,那么袋中共有个球.13. 不等式组 的解集为 .14. 如图,等腰三角形ABC中,已知AB=AC,∠A=30°,AB的垂直平分线交AC于D,则∠CBD的度数为°. 15. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 .
15. 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 .
三、解答题
-
16. 先化简,再求值: ,其中x=3tan30°+1.17. 如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.
 (1)、求证:△ADE≌△CBF;(2)、若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.18. 某市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四个品种的树苗共500株进行树苗成活率试验,从中选择成活率高的品种进行推广.通过实验得知:丙种树苗的成活率为89.6%,把实验数据绘制成下面两幅统计图(部分信息未给出).
(1)、求证:△ADE≌△CBF;(2)、若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.18. 某市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四个品种的树苗共500株进行树苗成活率试验,从中选择成活率高的品种进行推广.通过实验得知:丙种树苗的成活率为89.6%,把实验数据绘制成下面两幅统计图(部分信息未给出). (1)、实验所用的乙种树苗的数量是株.(2)、求出丙种树苗的成活数,并把图2补充完整.(3)、你认为应选哪种树苗进行推广?(4)、请通过计算说明理由.19. 钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48)
(1)、实验所用的乙种树苗的数量是株.(2)、求出丙种树苗的成活数,并把图2补充完整.(3)、你认为应选哪种树苗进行推广?(4)、请通过计算说明理由.19. 钓鱼岛自古就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测.一日,中国一艘海监船从A点沿正北方向巡航,其航线距钓鱼岛(设M,N为该岛的东西两端点)最近距离为14.4km(即MC=14.4km).在A点测得岛屿的西端点M在点A的北偏东42°方向;航行4km后到达B点,测得岛屿的东端点N在点B的北偏东56°方向,(其中N,M,C在同一条直线上),求钓鱼岛东西两端点MN之间的距离(结果精确到0.1km).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin56°≈0.83,cos56°≈0.56,tan56°≈1.48) 20. 如图,一次函数y=﹣x+4的图象与反比例y= (k为常数,且k≠0)的图象交于A(1,a),B两点.
20. 如图,一次函数y=﹣x+4的图象与反比例y= (k为常数,且k≠0)的图象交于A(1,a),B两点. (1)、求反比例函数的表达式及点B的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.21. 我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.(1)、若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?(2)、若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?(3)、在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.22. 在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE= ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)、求反比例函数的表达式及点B的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.21. 我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.(1)、若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?(2)、若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?(3)、在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.22. 在正方形ABCD中,对角线AC、BD交于点O,动点P在线段BC上(不含点B),∠BPE= ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G. (1)、当点P与点C重合时(如图①),求证:△BOG≌△POE;(2)、通过观察、测量、猜想: = ,并结合图②证明你的猜想;(3)、把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求 的值.(用含α的式子表示)23. 已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)、当点P与点C重合时(如图①),求证:△BOG≌△POE;(2)、通过观察、测量、猜想: = ,并结合图②证明你的猜想;(3)、把正方形ABCD改为菱形,其他条件不变(如图③),若∠ACB=α,求 的值.(用含α的式子表示)23. 已知:如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0). (1)、求该抛物线的解析式;(2)、点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(3)、若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;(3)、若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.