2016年江苏省泰州市兴化市顾庄学区三校联考中考数学三模试卷

试卷更新日期：2017-04-24 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣3的绝对值等于（）

A、3 B、 $\frac{1}{3}$ C、- $\frac{1}{3}$ D、﹣3

查看试题解析
2. 已知地球上海洋面积为316 000 000km² ，数据316 000 000用科学记数法表示为（）

A、3.61×10⁹ B、3.61×10⁸ C、3.61×10⁷ D、3.61×10⁶

查看试题解析
3. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是（　　）

A、7 B、8 C、9 D、10

查看试题解析
4. 如图所示的几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 某班25名女学生在一次“1分钟仰卧起坐”测试中，成绩如表：
成绩（次）
43
45
46
47
48
49
51
人数
2
3
5
7
4
2
2
则这25名女生测试成绩的众数和中位数分别是（）

A、47，46 B、47，47 C、45，48 D、7，3

查看试题解析
6. 如图，在平面直角坐标系中，点B在y轴上，第一象限内点A满足AB=AO，反比例函数y= $\frac{k}{x}$ 的图象经过点A，若△ABO的面积为2，则k的值为（）

A、1 B、2 C、4 D、 $\frac{1}{2}$

查看试题解析

二、填空题

7. 若y= $\sqrt{3 - x}$ 有意义，则x的取值范围是．

查看试题解析
8. 如图，转盘中8个扇形的面积都相等，任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为．

查看试题解析
9. 如图，直线l₁∥l₂∥l₃ ，等边△ABC的顶点B、C分别在直线l₂、l₃上，若边BC与直线l₃的夹角∠1=25°，则边AB与直线l₁的夹角∠2= ．

查看试题解析
10. 将抛物线y=2x²﹣1向右平移4个单位后，所得抛物线相应的函数表达式是．

查看试题解析
11. 若代数式x²﹣3x+2可以表示为（x+1）²+a（x+1）+b的形式，则a﹣b的值是．

查看试题解析
12. 若某个圆锥的侧面积为8πcm² ，其侧面展开图的圆心角为45°，则该圆锥的底面半径为 cm．

查看试题解析
13. 如图，已知△ABC的三个顶点均在格点上，则cosA的值为．

查看试题解析
14. 如图，点C在⊙O的直径AB上，AB=6，AC=1．点P为⊙O上的任意一点，当∠OPC取最大值时，则△OCP的面积为．

查看试题解析

三、解答题

15. 解答题。

(1)、计算：|﹣2|﹣ $\sqrt{\frac{1}{16}}$ +（﹣2）^﹣²﹣（ $\sqrt{3} - 2$ ）⁰；

(2)、解不等式组 ${\begin{matrix} 2 - x \leq 3 \\ \frac{3}{2} x + 1 > x - \frac{3}{2} \end{matrix}$ ，并求其最小整数解．

查看试题解析
16. 先化简，再求值：（ $\frac{x^{2}}{x - 1}$ ﹣ $\frac{x^{2}}{x^{2} - 1}$ ）÷ $\frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，其中x是方程3x²﹣x﹣1=0的根．

查看试题解析
17. 学校为统筹安排大课间体育活动，在各班随机选取了一部分学生，分成四类活动：“篮球”、“羽毛球”、“乒乓球”、“其他”进行调查，整理收集到的数据，绘制成如下的两幅统计图．

(1)、学校采用的调查方式是；学校共选取了名学生；

(2)、补全统计图中的数据：条形统计图中羽毛球人、乒乓球人、其他人、扇形统计图中其他 %；

(3)、该校共有1100名学生，请估计喜欢“篮球”的学生人数．

查看试题解析
18. 如图，在△ABC中，AB=AC，∠DAC是△ABC的一个外角．
实验与操作：
根据要求进行尺规作图，并在图中标明相应字母（保留作图痕迹，不写作法）

(1)、作∠DAC的平分线AM；

(2)、作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE，CF．猜想并证明：
判断四边形AECF的形状并加以证明．

查看试题解析
19. 宁波火车站北广场将于2015年底投入使用，计划在广场内种植A，B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵

(1)、A，B两种花木的数量分别是多少棵？

(2)、如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？

查看试题解析
20. 如图1，一条细绳系着一个小球在平面内摆动，已知细绳从悬挂点O到球心的长度为50厘米，小球在带你B位置时达到最低点，当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°．（取sin37°=0.6，cos37°=0.8，tan37°=0.75）

(1)、求点A与点B的高度差BC的值．

(2)、如图2，若在点O的正下方有一个阻碍物P，当小球从左往右落到最低处后，运动轨迹改变，变为以P为圆心，PB为半径继续向右摆动，当摆动至与点A在同一水平高度的点D时，满足PD部分细绳与水平线的夹角∠DPQ=30°，求OP的长度．

查看试题解析
21. 如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为BC边上的点，反比例函数y= $\frac{k}{x}$ （k≠0）在第一象限内的图象经过点D（m，2）和AB边上的点E（3， $\frac{2}{3}$ ）．

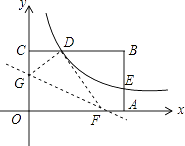(1)、求反比例函数的表达式和m的值；

(2)、将矩形OABC的进行折叠，使点O于点D重合，折痕分别与x轴、y轴正半轴交于点F，G，求折痕FG所在直线的函数关系式．

查看试题解析
22.
如图，点E为正方形ABCD中AD边上的一个动点，AB=16，以BE为边画正方形BEFG，边EF与边CD交于点H．

(1)、当E为边AD的中点时，求DH的长；

(2)、当tan∠ABE= $\frac{3}{4}$ 时，连接CF，求CF的长；

(3)、连接CE，求△CEF面积的最小值．

查看试题解析
23.
如图1，在以O为原点的平面直角坐标系中，点A的坐标为（0，2），点P（s，t）在抛物线y= $\frac{1}{4}$ x²+1上，点P到x轴的距离记为m，PA=n．

(1)、若s=4，分别求出m、n的值，并比较m与n的大小关系；

(2)、若点P是该抛物线上的一个动点，则（1）中m与n的大小关系是否仍成立？请说明理由；

(3)、如图2，过点P的直线y=kx（k≠0）与抛物线交于另一点Q连接PA、QA，是否存在k使得PA=2QA？若存在，请求出k的值；若不存在，请举例说明．

查看试题解析

成绩（次）	43	45	46	47	48	49	51
人数	2	3	5	7	4	2	2