2016年黑龙江省哈尔滨市平房区中考数学模拟试卷(三)
试卷更新日期:2017-04-24 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、﹣ B、 C、 D、﹣2. 下列运算,正确的是( )A、a+a3=a4 B、a2•a3=a6 C、(a2)3=a6 D、a10÷a2=a53. 观察下列图案,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个动点,过A点作y轴的平行线交反比例函数y= (x>0)的图象于B点,当点A的横坐标逐渐增大时,△OAB的面积将会( )A、逐渐增大 B、逐渐减小 C、不变 D、先增大后减小5. 如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )
4. 在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个动点,过A点作y轴的平行线交反比例函数y= (x>0)的图象于B点,当点A的横坐标逐渐增大时,△OAB的面积将会( )A、逐渐增大 B、逐渐减小 C、不变 D、先增大后减小5. 如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )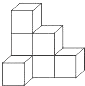 A、
A、 B、
B、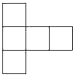 C、
C、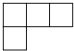 D、
D、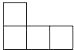 6. 某公司去年的利润(总产值﹣总支出)为200万元.今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.如果去年的总产值x万元、总支出y万元,则下列方程组正确的是( )A、 B、 C、 D、7. △ABC中,∠A、∠B都是锐角,且sinA= ,cosB= ,则△ABC的形状是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定8. 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( )
6. 某公司去年的利润(总产值﹣总支出)为200万元.今年总产值比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元.如果去年的总产值x万元、总支出y万元,则下列方程组正确的是( )A、 B、 C、 D、7. △ABC中,∠A、∠B都是锐角,且sinA= ,cosB= ,则△ABC的形状是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、不能确定8. 如图在△ABC中,DE∥BC,DF∥AC,则下列比例式不正确的是( ) A、 = B、 = C、 = D、 =9. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A、 = B、 = C、 = D、 =9. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )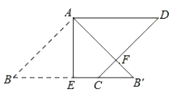 A、1 B、 C、2- D、2 ﹣210. 小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离y(m)与时间x(s)的函数关系图象是( )A、
A、1 B、 C、2- D、2 ﹣210. 小明为准备体育中考,每天早晨坚持锻炼,某天他慢跑到江边,休息一会后快跑回家,能大致反映小明离家的距离y(m)与时间x(s)的函数关系图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 哈南公共自行车的投用给平房人带来很多便利,受到居民的普遍欢迎,目前租车次数已经超过1019000次.将1019000用科学记数法表示为 .12. 函数 中,自变量x的取值范围是 .13. 计算: ÷ = .14. 因式分解:a3+2a2+a= .15. 如图,一张圆心角为45°的扇形纸板剪得一个边长为1的正方形,则扇形纸板的面积是 cm2(结果保留π)
 16. 不等式组 的正整数解是 .17. 有两组卡片,第一组的三张卡片上分别写有数字3,4,5,第二组的三张卡片上分别写有数字1,3,5,现从每组卡片中各随机抽出一张,用抽取的第一组卡片的数字减去抽取的第二组卡片上的数字,差为正数的概率为 .18. ⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2﹣4x+m=0的两根,当直线l与⊙O相切时,m的值为 .19. 用直角边分别为6和8的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是 .20. 如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF= .
16. 不等式组 的正整数解是 .17. 有两组卡片,第一组的三张卡片上分别写有数字3,4,5,第二组的三张卡片上分别写有数字1,3,5,现从每组卡片中各随机抽出一张,用抽取的第一组卡片的数字减去抽取的第二组卡片上的数字,差为正数的概率为 .18. ⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2﹣4x+m=0的两根,当直线l与⊙O相切时,m的值为 .19. 用直角边分别为6和8的两个直角三角形拼成一个平行四边形(非矩形),所得的平行四边形的周长是 .20. 如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF= .
三、解答题
-
21. 先化简,再求值:( ﹣ )÷ ,其中x=2sin30°+ tan30°.22. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(5,1).
①画出△ABC关于y轴对称的△A1B1C1 , 并写出点C1的坐标;
②连结BC1 , 在坐标平面的格点上确定一个点P,使△B C1P是以B C1为底的等腰直角三角形,画出△B C1P,并写出所有P点的坐标.
 23. 端午节快到了,某市共青团组织以“中学生最喜欢项节日活动”为主题题进行了简单的随机抽样调查,让学生从“郊外踏青、品尝美食、观赏电影、参观室馆”四项活动中选择一项,然后绘制出以下两幅不完整的统计图.请根据图中的信息,回答下列问题:
23. 端午节快到了,某市共青团组织以“中学生最喜欢项节日活动”为主题题进行了简单的随机抽样调查,让学生从“郊外踏青、品尝美食、观赏电影、参观室馆”四项活动中选择一项,然后绘制出以下两幅不完整的统计图.请根据图中的信息,回答下列问题: (1)、这次抽样调查中共调查了人;扇形统计图中郊外踏青部分的圆心角的度数是°;(2)、请补全条形统计图;(3)、某市有中学生3万人,请估计选择郊外踏青的人数有多少?24. 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F.
(1)、这次抽样调查中共调查了人;扇形统计图中郊外踏青部分的圆心角的度数是°;(2)、请补全条形统计图;(3)、某市有中学生3万人,请估计选择郊外踏青的人数有多少?24. 如图,四边形ABCD是平行四边形,BE、DF分别是∠ABC、∠ADC的平分线,且与对角线AC分别相交于点E、F. (1)、求证:AE=CF;(2)、连结ED、FB,判断四边形BEDF是否是平行四边形,说明理由.25. 学校计划从商店购买同一品牌的钢笔和文具盒,已知购买一个文具盒比购买一个钢笔多用20元,若用400元购买文具盒和用160元购买钢笔,则购买文具盒的个数是购买钢笔个数的一半.(1)、分别求出该品牌文具盒、钢笔的定价;(2)、经商谈,商店给予学校购买一个该品牌文具盒赠送一个该品牌钢笔的优惠,如果学校需要钢笔的个数是文具盒个数的2倍还多8个,且学校购买文具盒和钢笔的总费用不超过670元,那么该学校最多可购买多少个该品牌文具盒?26. 在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD.
(1)、求证:AE=CF;(2)、连结ED、FB,判断四边形BEDF是否是平行四边形,说明理由.25. 学校计划从商店购买同一品牌的钢笔和文具盒,已知购买一个文具盒比购买一个钢笔多用20元,若用400元购买文具盒和用160元购买钢笔,则购买文具盒的个数是购买钢笔个数的一半.(1)、分别求出该品牌文具盒、钢笔的定价;(2)、经商谈,商店给予学校购买一个该品牌文具盒赠送一个该品牌钢笔的优惠,如果学校需要钢笔的个数是文具盒个数的2倍还多8个,且学校购买文具盒和钢笔的总费用不超过670元,那么该学校最多可购买多少个该品牌文具盒?26. 在⊙O中,弦AB、CD相交于点E,连接AC、BC,AC=BC,AB=CD. (1)、如图1,求证:BE平分∠CBD;(2)、如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ∠ACB时,求证:AC=BD+2CF;(3)、如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ,求线段GD的长.27. 在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C.
(1)、如图1,求证:BE平分∠CBD;(2)、如图2,F为BC上一点,连接AF交CD于点G,当∠FAB= ∠ACB时,求证:AC=BD+2CF;(3)、如图3,在(2)的条件下,若S△ACF=S△CBD , ⊙O的半径为3 ,求线段GD的长.27. 在平面直角坐标系中,抛物线y=ax2﹣5ax+4a与x轴交于A、B(A点在B点的左侧)与y轴交于点C. (1)、如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;(2)、如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;(3)、如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 a,连接KB并延长交抛物线于点Q,求PQ的长.
(1)、如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;(2)、如图2,点P为第四象限抛物线上一点,连接PC,若∠BCP=2∠ABC时,求点P的横坐标;(3)、如图3,在(2)的条件下,点F在AP上,过点P作PH⊥x轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=﹣4 a,连接KB并延长交抛物线于点Q,求PQ的长.