2016年安徽省合肥市高新区中考数学二模试卷
试卷更新日期:2017-04-24 类型:中考模拟
一、选择题
-
1. ﹣2的相反数是( )A、2 B、1 C、 D、﹣2. 如图是由四个相同的小立方体组成的立体图形的主视图和左视图,那么这个立体图形不可能是( )
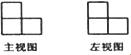 A、
A、 B、
B、 C、
C、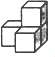 D、
D、 3. 下列计算正确的是( )A、4x2+2x2=6x4 B、(x﹣y)2=x2﹣y2 C、(x3)2=x5 D、x2•x2=x44. 2016年2月初,合肥市教育考试院召开新闻发布会,公布了合肥市市区参加2016年中考的学生约为27600人,与去年相比增加300多人,用科学记数法表示“27600”正确的( )A、2.76×103 B、2.76×104 C、2.76×105 D、0.276×1055. 如图,已知AB∥DE,∠ABC=65°,∠CDE=138°,则∠C的值为( )
3. 下列计算正确的是( )A、4x2+2x2=6x4 B、(x﹣y)2=x2﹣y2 C、(x3)2=x5 D、x2•x2=x44. 2016年2月初,合肥市教育考试院召开新闻发布会,公布了合肥市市区参加2016年中考的学生约为27600人,与去年相比增加300多人,用科学记数法表示“27600”正确的( )A、2.76×103 B、2.76×104 C、2.76×105 D、0.276×1055. 如图,已知AB∥DE,∠ABC=65°,∠CDE=138°,则∠C的值为( )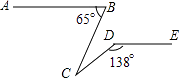 A、21° B、23° C、25° D、30°6. “国庆黄金周”期间,小东和爸爸、妈妈外出旅游,一家三人随机站在一排拍照纪念,小东恰好站在中间的概率是( )A、 B、 C、 D、7. 甲、乙两个车站相距96千米,快车和慢车同时从甲站开出,1小时后快车在慢车前12千米,快车比慢车早40分钟到达乙站,快车和慢车的速度各是多少?设快车的速度为x千米/时,则下列方程正确的是( )A、 B、 =40 C、 D、8. 如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则 的值等于( )
A、21° B、23° C、25° D、30°6. “国庆黄金周”期间,小东和爸爸、妈妈外出旅游,一家三人随机站在一排拍照纪念,小东恰好站在中间的概率是( )A、 B、 C、 D、7. 甲、乙两个车站相距96千米,快车和慢车同时从甲站开出,1小时后快车在慢车前12千米,快车比慢车早40分钟到达乙站,快车和慢车的速度各是多少?设快车的速度为x千米/时,则下列方程正确的是( )A、 B、 =40 C、 D、8. 如图所示,△ABC是等边三角形,点D为AB上一点,现将△ABC沿EF折叠,使得顶点A与D点重合,且FD⊥BC,则 的值等于( )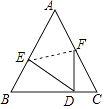 A、 B、 C、 D、9. 如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )
A、 B、 C、 D、9. 如图,原有一大长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若原来该大长方形的周长是120,则分割后不用测量就能知道周长的图形标号为( )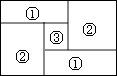 A、①② B、②③ C、①③ D、①②③10. 一元二次方程m1x2+ x+1=0的两根分别为x1 , x2 , 一元二次方程m2x2+ x+1=0的两根为x3 , x4 , 若x1<x3<x4<x2<0,则m1 , m2的大小关系为( )A、0>m1>m2 B、0>m2>m1 C、m2>m1>0 D、m1>m2>0
A、①② B、②③ C、①③ D、①②③10. 一元二次方程m1x2+ x+1=0的两根分别为x1 , x2 , 一元二次方程m2x2+ x+1=0的两根为x3 , x4 , 若x1<x3<x4<x2<0,则m1 , m2的大小关系为( )A、0>m1>m2 B、0>m2>m1 C、m2>m1>0 D、m1>m2>0二、填空题
-
11. 化简: ﹣ = .12. 若函数y= ,则当函数值y=15时,自变量x的值是 .13. 观察下列图形规律:当n=时,图形“△”的个数是“●”的个数的2倍.
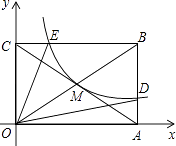
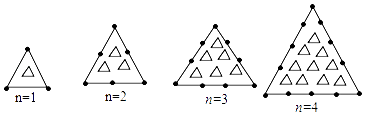 14. 如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).
14. 如图,反比例函数y= (x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E.,则下列结论正确的是(将正确的结论填在横线上).①s△OEB=s△ODB , ②BD=4AD,③连接MD,S△ODM=2S△OCE , ④连接ED,则△BED∽△BCA.
三、解答题。
-
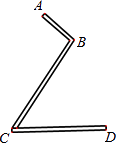
15. 先化简,再求值: ,其中a=﹣2.16. 求不等式 x﹣1>3x的解集,并判断x=﹣ 是否为此不等式的解.17. 现有一个“Z”型的工件(工件厚度忽略不计),如图示,其中AB为20cm,BC为60cm,∠ABC=90°,∠BCD=50°,求该工件如图摆放时的高度(即A到CD的距离).(结果精确到0.1m,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
 18. 在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),
18. 在平面直角坐标系中,点A、B的坐标分别是(0,3)、(﹣4,0),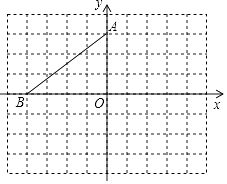 (1)、将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;(2)、以O点为位似中心,将△AEF作位似变换且缩小为原来的 ,在网格内画出一个符合条件的△A1E1F1 .19. 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣ ,3 ),AB=2,AD=3.
(1)、将△AOB绕点A逆时针旋转90°得到△AEF,点O,B对应点分别是E,F,请在图中画出△AEF,并写出E、F的坐标;(2)、以O点为位似中心,将△AEF作位似变换且缩小为原来的 ,在网格内画出一个符合条件的△A1E1F1 .19. 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(﹣ ,3 ),AB=2,AD=3.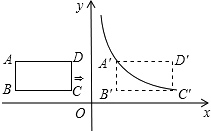 (1)、直接写出B、C、D三点的坐标;(2)、将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.20. 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
(1)、直接写出B、C、D三点的坐标;(2)、将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数y= (x>0)的图象上,得矩形A'B'C'D'.求矩形ABCD的平移距离m和反比例函数的解析式.20. 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.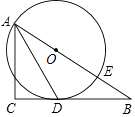 (1)、求证:AD平分∠BAC;(2)、若AC=8,tan∠DAC= ,求⊙O的半径.21. 某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.
(1)、求证:AD平分∠BAC;(2)、若AC=8,tan∠DAC= ,求⊙O的半径.21. 某省是劳务输出大省,农民外出务工增长家庭收入的同时,也一定程度影响了子女的管理和教育,缺少管理和教育的留守儿童的学习和心理健康状况等问题日趋显现,成为社会关注的焦点.该省相关部门就留守儿童学习和心理健康状况等问题进行调查,本次抽样调查了该省某县部分留守儿童,将调查出现的情况分四类,即A类:基本情况正常;B类;有轻度问题;C类:有较为严重问题;D类:有特别严重问题.通过调查,得到下面两幅不完整的统计图,请根据图中的信息解决下面的问题.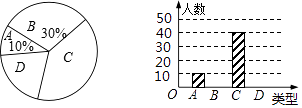 (1)、在这次随机抽样调查中,共抽查了多少名学生留守儿童?(2)、扇形统计图中C类所占的圆心角是°;这次调查中为D类的留守儿童有人;(3)、请你估计该县20000名留守儿童中,出现较为严重问题及以上的人数.22. 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190﹣2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
(1)、在这次随机抽样调查中,共抽查了多少名学生留守儿童?(2)、扇形统计图中C类所占的圆心角是°;这次调查中为D类的留守儿童有人;(3)、请你估计该县20000名留守儿童中,出现较为严重问题及以上的人数.22. 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190﹣2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.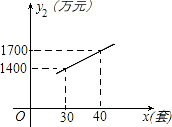 (1)、直接写出y2(2)与x之间的函数关系式;(2)、求月产量x的取值范围;(3)、当月产量x(套)为多少时,这种产品的利润W(万元)最大?最大利润是多少?23.
(1)、直接写出y2(2)与x之间的函数关系式;(2)、求月产量x的取值范围;(3)、当月产量x(套)为多少时,这种产品的利润W(万元)最大?最大利润是多少?23.如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB•AD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
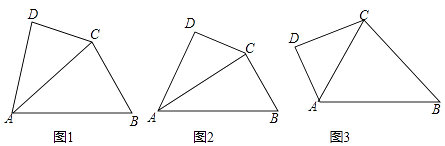 (1)、如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;(2)、如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;(3)、现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
(1)、如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;(2)、如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;(3)、现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .