2014年浙江省湖州市中考数学试卷
试卷更新日期:2017-04-24 类型:中考真卷
一、选择题
-
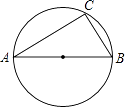
1. ﹣3的倒数是( )A、﹣3 B、3 C、 D、﹣2. 2014•湖州)计算2x(3x2+1),正确的结果是( )A、5x3+2x B、6x3+1 C、6x3+2x D、6x2+2x3. 二次根式 中字母x的取值范围是( )A、x<1 B、x≤1 C、x>1 D、x≥14. 如图,已知AB是△ABC外接圆的直径,∠A=35°,则∠B的度数是( )
 A、35° B、45° C、55° D、65°5. 数据﹣2,﹣1,0,1,2的方差是( )A、0 B、 C、2 D、46. 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC的长是( )
A、35° B、45° C、55° D、65°5. 数据﹣2,﹣1,0,1,2的方差是( )A、0 B、 C、2 D、46. 如图,已知Rt△ABC中,∠C=90°,AC=4,tanA= ,则BC的长是( ) A、2 B、8 C、2 D、47. 已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )A、1 B、2 C、3 D、48. 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= AB中,一定正确的是( )
A、2 B、8 C、2 D、47. 已知一个布袋里装有2个红球,3个白球和a个黄球,这些球除颜色外其余都相同.若从该布袋里任意摸出1个球,是红球的概率为 ,则a等于( )A、1 B、2 C、3 D、48. 如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①ED⊥BC;②∠A=∠EBA;③EB平分∠AED;④ED= AB中,一定正确的是( ) A、①②③ B、①②④ C、①③④ D、②③④9. 如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3 , 则下列结论不一定成立的是( )
A、①②③ B、①②④ C、①③④ D、②③④9. 如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3 , 则下列结论不一定成立的是( ) A、S1>S2+S3 B、△AOM∽△DMN C、∠MBN=45° D、MN=AM+CN10. 在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )A、
A、S1>S2+S3 B、△AOM∽△DMN C、∠MBN=45° D、MN=AM+CN10. 在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )A、 B、
B、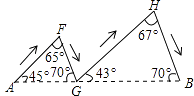 C、
C、 D、
D、
二、填空题
-
11. 方程2x﹣1=0的解是x= .12. 如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
 13. 计算:50°﹣15°30′= .14. 下面的频数分布折线图分别表示我国A市与B市在2014年4月份的日平均气温的情况,记该月A市和B市日平均气温是8℃的天数分别为a天和b天,则a+b= .
13. 计算:50°﹣15°30′= .14. 下面的频数分布折线图分别表示我国A市与B市在2014年4月份的日平均气温的情况,记该月A市和B市日平均气温是8℃的天数分别为a天和b天,则a+b= . 15. 如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y= (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
15. 如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y= (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 . 16. 已知当x1=a,x2=b,x3=c时,二次函数y= x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .
16. 已知当x1=a,x2=b,x3=c时,二次函数y= x2+mx对应的函数值分别为y1 , y2 , y3 , 若正整数a,b,c恰好是一个三角形的三边长,且当a<b<c时,都有y1<y2<y3 , 则实数m的取值范围是 .三、解答题
-
17. 计算:(3+a)(3﹣a)+a2 .18. 解方程组 .19. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
 (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.20. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 的图象上,过点A的直线y=x+b交x轴于点B.
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.20. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y= 的图象上,过点A的直线y=x+b交x轴于点B.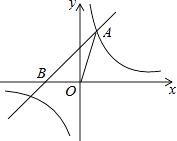 (1)、求k和b的值;(2)、求△OAB的面积.21.
(1)、求k和b的值;(2)、求△OAB的面积.21.已知2014年3月份在某医院出生的20名新生婴儿的体重如下(单位:kg)
4.7 2.9 3.2 3.5 3.8 3.4 2.8 3.3 4.0 4.5
3.6 4.8 4.3 3.6 3.4 3.5 3.6 3.5 3.7 3.7
 (1)、求这组数据的极差;(2)、若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量
(1)、求这组数据的极差;(2)、若以0.4kg为组距,对这组数据进行分组,制作了如下的“某医院2014年3月份20名新生婴儿体重的频数分布表”(部分空格未填),请在频数分布表的空格中填写相关的量某医院2014年3月份20名新生儿体重的频数分布表
组别(kg)
划记
频数
略
略
3.55﹣3.95
正一
6
略
略
略
合计
20
(3)、经检测,这20名婴儿的血型的扇形统计图如图所示(不完整),求:①这20名婴儿中是A型血的人数;
②表示O型血的扇形的圆心角度数.
22. 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.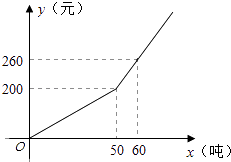 (1)、当x≥50时,求y关于x的函数关系式;(2)、若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;(3)、为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.23.
(1)、当x≥50时,求y关于x的函数关系式;(2)、若某企业2013年10月份的水费为620元,求该企业2013年10月份的用水量;(3)、为贯彻省委“五水共治”发展战略,鼓励企业节约用水,该市自2014年1月开始对月用水量超过80吨的企业加收污水处理费,规定:若企业月用水量x超过80吨,则除按2013年收费标准收取水费外,超过80吨部分每吨另加收 元,若某企业2014年3月份的水费和污水处理费共600元,求这个企业该月的用水量.23.如图,已知在平面直角坐标系xOy中,O是坐标原点,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C,过点C作CA∥x轴交抛物线于点A,在AC延长线上取点B,使BC= AC,连接OA,OB,BD和AD.
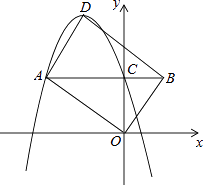 (1)、若点A的坐标是(﹣4,4).
(1)、若点A的坐标是(﹣4,4).①求b,c的值;
②试判断四边形AOBD的形状,并说明理由;
(2)、是否存在这样的点A,使得四边形AOBD是矩形?若存在,请直接写出一个符合条件的点A的坐标;若不存在,请说明理由.24. 已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点P作PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0). (1)、若点E在y轴的负半轴上(如图所示),求证:PE=PF;(2)、在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;(3)、作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.
(1)、若点E在y轴的负半轴上(如图所示),求证:PE=PF;(2)、在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;(3)、作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.