2013年浙江省义乌市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

1. 在2，﹣2，8，6这四个数中，互为相反数的是（）

A、﹣2与2 B、2与8 C、﹣2与6 D、6与8

查看试题解析
2. 如图几何体的主视图是（）

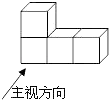A、 B、 C、 D、

查看试题解析
3. 如图，直线a∥b，直线c与a、b相交，∠1=55°，则∠2=（）

A、55° B、35° C、125° D、65°

查看试题解析
4. 2012年，义乌市城市居民人均可支配收入约为44500元，居全省县级市之首，数字44500用科学记数法可表示为（）

A、4.45×10³ B、4.45×10⁴ C、4.45×10⁵ D、4.45×10⁶

查看试题解析
5. 两圆的半径分别为3和5，圆心距为7，则两圆的位置关系是（）

A、内切 B、相交 C、外切 D、外离

查看试题解析
6. 已知两点P₁（x₁ ， y₁）、P₂（x₂、y₂）在反比例函数y= $\frac{3}{x}$ 的图象上，当x₁＞x₂＞0时，下列结论正确的是（）

A、0＜y₁＜y₂ B、0＜y₂＜y₁ C、y₁＜y₂＜0 D、y₂＜y₁＜0

查看试题解析
7. 下列图形中，既是轴对称图形又是中心对称图形的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 已知圆锥的底面半径为6cm，高为8cm，则这个圆锥的母线长为（）

A、12cm B、10cm C、8cm D、6cm

查看试题解析
9. 为支援雅安灾区，小慧准备通过爱心热线捐款，她只记得号码的前5位，后三位由5，1，2，这三个数字组成，但具体顺序忘记了，他第一次就拨通电话的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
10. 如图，抛物线y=ax²+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点），则下列结论：
①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣ $\frac{2}{3}$ ；④3≤n≤4中，
正确的是（）

A、①② B、③④ C、①④ D、①③

查看试题解析

二、填空题

11. 把角度化为度、分的形式，则20.5°=20°′．

查看试题解析
12. 计算：3a•a²+a³= ．

查看试题解析
13. 若数据2，3，﹣1，7，x的平均数为2，则x= ．

查看试题解析
14. 如图，已知∠B=∠C，添加一个条件使△ABD≌△ACE（不标注新的字母，不添加新的线段），你添加的条件是．

查看试题解析
15. 如图，AD⊥BC于点D，D为BC的中点，连接AB，∠ABC的平分线交AD于点O，连结OC，若∠AOC=125°，则∠ABC= ．

查看试题解析
16.
如图，直线l₁⊥x轴于点A（2，0），点B是直线l₁上的动点．直线l₂：y=x+1交l₁于点C，过点B作直线l₃垂直于l₂ ，垂足为D，过点O，B的直线l₄交l₂于点E，当直线l₁ ， l₂ ， l₃能围成三角形时，设该三角形面积为S₁ ，当直线l₂ ， l₃ ， l₄能围成三角形时，设该三角形面积为S₂ ．

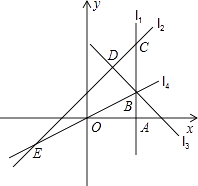(1)、若点B在线段AC上，且S₁=S₂ ，则B点坐标为；

(2)、若点B在直线l₁上，且S₂= $\sqrt{3}$ S₁ ，则∠BOA的度数为．

查看试题解析

三、解答题

17. 计算：（π﹣3.14）⁰+（ $\frac{1}{2}$ ）^﹣¹+|﹣2 $\sqrt{2}$ |﹣ $\sqrt{8}$ ．

查看试题解析
18. 解方程

(1)、x²﹣2x﹣1=0

(2)、 $\frac{2}{x}$ = $\frac{3}{2 x - 1}$ ．

查看试题解析
19. 如图1所示，从边长为a的正方形纸片中剪去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸拼成如图2的等腰梯形，

(1)、设图1中阴影部分面积为S₁ ，图2中阴影部分面积为S₂ ，请直接用含a、b的代数式表示S₁和S₂；

(2)、请写出上述过程所揭示的乘法公式．

查看试题解析
20. 在义乌市中小学生“我的中国梦”读书活动中，某校对部分学生做了一次主题为：“我最喜爱的图书”的调查活动，将图书分为甲、乙、丙、丁四类，学生可根据自己的爱好任选其中一类．学校根据调查情况进行了统计，并绘制了不完整的条形统计图和扇形统计图．
请你结合图中信息，解答下列问题：

(1)、本次共调查了名学生；

(2)、被调查的学生中，最喜爱丁类图书的学生有人，最喜爱甲类图书的人数占本次被调查人数的 %；

(3)、在最喜爱丙类图书的学生中，女生人数是男生人数的1.5倍，若这所学校共有学生1500人，请你估计该校最喜爱丙类图书的女生和男生分别有多少人？

查看试题解析
21. 已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．

(1)、若⊙O的半径为8，求CD的长；

(2)、证明：PE=PF；

(3)、若PF=13，sinA= $\frac{5}{13}$ ，求EF的长．

查看试题解析
22. 为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．
采购数量（件）
1
2
…
A产品单价（元/件）
1480
1460
…
B产品单价（元/件）
1290
1280
…

(1)、设A产品的采购数量为x（件），采购单价为y₁（元/件），求y₁与x的关系式；

(2)、经商家与厂家协商，采购A产品的数量不少于B产品数量的 $\frac{11}{9}$ ，且A产品采购单价不低于1200元，求该商家共有几种进货方案；

(3)、该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．

查看试题解析
23.
小明合作学习小组在探究旋转、平移变换．如图△ABC，DEF均为等腰直角三角形，各顶点坐标分别为A（1，1），B（2，2），C（2，1），D（ $\sqrt{2}$ ，0），E（2 $\sqrt{2}$ ，0），F（ $\frac{3 \sqrt{2}}{2}$ ，﹣ $\frac{\sqrt{2}}{2}$ ）．

(1)、他们将△ABC绕C点按顺时针方向旋转45°得到△A₁B₁C₁ ．请你写出点A₁ ， B₁的坐标，并判断A₁C和DF的位置关系；

(2)、他们将△ABC绕原点按顺时针方向旋转45°，发现旋转后的三角形恰好有两个顶点落在抛物线y=2 $\sqrt{2}$ x²+bx+c上，请你求出符合条件的抛物线解析式；

(3)、他们继续探究，发现将△ABC绕某个点旋转45°，若旋转后的三角形恰好有两个顶点落在抛物线y=x²上，则可求出旋转后三角形的直角顶点P的坐标，请你直接写出点P的所有坐标．

查看试题解析
24.
如图1所示，已知y= $\frac{6}{x}$ （x＞0）图象上一点P，PA⊥x轴于点A（a，0），点B坐标为（0，b）（b＞0），动点M是y轴正半轴上B点上方的点，动点N在射线AP上，过点B作AB的垂线，交射线AP于点D，交直线MN于点Q连接AQ，取AQ的中点为C．

(1)、如图2，连接BP，求△PAB的面积；

(2)、当点Q在线段BD上时，若四边形BQNC是菱形，面积为2 $\sqrt{3}$ ，求此时P点的坐标；

(3)、当点Q在射线BD上时，且a=3，b=1，若以点B，C，N，Q为顶点的四边形是平行四边形，求这个平行四边形的周长．

查看试题解析

采购数量（件）	1	2	…
A产品单价（元/件）	1480	1460	…
B产品单价（元/件）	1290	1280	…