2013年浙江省温州市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

1. 计算：（﹣2）×3的结果是（）

A、﹣6 B、﹣1 C、1 D、6

查看试题解析
2. 小明对九（1）班全班同学“你最喜欢的球类项目是什么？（只选一项）”的问题进行了调查，把所得数据绘制成如图所示的扇形统计图，由图可知，该班同学最喜欢的球类项目是（）

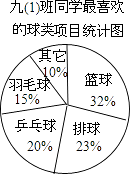A、羽毛球 B、乒乓球 C、排球 D、篮球

查看试题解析
3. 下列各图中，经过折叠能围成一个立方体的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各组数可能是一个三角形的边长的是（）

A、1，2，4 B、4，5，9 C、4，6，8 D、5，5，11

查看试题解析
5. 若分式 $\frac{x - 3}{x + 4}$ 的值为0，则x的值是（）

A、x=3 B、x=0 C、x=﹣3 D、x=﹣4

查看试题解析
6. 已知点P（1，﹣3）在反比例函数y= $\frac{k}{x}$ （k≠0）的图象上，则k的值是（）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
7. 如图，在⊙O中，OC⊥弦AB于点C，AB=4，OC=1，则OB的长是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{15}$ D、 $\sqrt{17}$

查看试题解析
8. 如图，在△ABC中，∠C=90°，AB=5，BC=3，则sinA的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
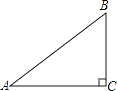9. 如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE=6， $\frac{A D}{B D} = \frac{3}{4}$ ，则EC的长是（）

A、4.5 B、8 C、10.5 D、14

查看试题解析
10. 在△ABC中，∠C为锐角，分别以AB，AC为直径作半圆，过点B，A，C作 $\hat{B A C}$ ，如图所示．若AB=4，AC=2，S₁﹣S₂= $\frac{π}{4}$ ，则S₃﹣S₄的值是（）

A、 $\frac{29 π}{4}$ B、 $\frac{23 π}{4}$ C、 $\frac{11 π}{4}$ D、 $\frac{5 π}{4}$

查看试题解析

二、填空题

11. 因式分解：m²﹣5m= ．

查看试题解析
12. 在演唱比赛中，5位评委给一位歌手的打分如下：8.2分，8.3分，7.8分，7.7分，8.0分，则这位歌手的平均得分是分．

查看试题解析
13. 如图，直线a，b被直线c所截，若a∥b，∠1=40°，∠2=70°，则∠3=度．

查看试题解析
14. 方程x²﹣2x﹣1=0的解是．

查看试题解析
15.
如图，在平面直角坐标系中，△ABC的两个顶点A，B的坐标分别为（﹣2，0），（﹣1，0），BC⊥x轴，将△ABC以y轴为对称轴作轴对称变换，得到△A′B′C′（A和A′，B和B′，C和C′分别是对应顶点），直线y=x+b经过点A，C′，则点C′的坐标是．

查看试题解析
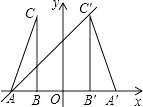16. 一块矩形木板，它的右上角有一个圆洞，现设想将它改造成火锅餐桌桌面，要求木板大小不变，且使圆洞的圆心在矩形桌面的对角线的交点上．木工师傅想了一个巧妙的办法，他测量了PQ与圆洞的切点K到点B的距离及相关数据（单位：cm），从点N沿折线NF﹣FM（NF∥BC，FM∥AB）切割，如图1所示．图2中的矩形EFGH是切割后的两块木板拼接成符合要求的矩形桌面示意图（不重叠，无缝隙，不记损耗），则CN，AM的长分别是．

查看试题解析

三、解答题

17. 计算下列各题

(1)、计算： $\sqrt{8}$ +（ $\sqrt{2}$ -1）+（ $\frac{1}{2}$ ）⁰

(2)、化简：（1+a）（1﹣a）+a（a﹣3）

查看试题解析
18. 如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

(1)、求证：△ACD≌△AED；

(2)、若∠B=30°，CD=1，求BD的长．

查看试题解析
19.
如图，在方格纸中，△ABC的三个顶点和点P都在小方格的顶点上，按要求画一个三角形，使它的顶点在方格的顶点上．

(1)、将△ABC平移，使点P落在平移后的三角形内部，在图甲中画出示意图；

(2)、以点C为旋转中心，将△ABC旋转，使点P落在旋转后的三角形内部，在图乙中画出示意图．

查看试题解析
20. 如图，抛物线y=a（x﹣1）²+4与x轴交于点A，B，与y轴交于点C，过点C作CD∥x轴交抛物线的对称轴于点D，连接BD，已知点A的坐标为（﹣1，0）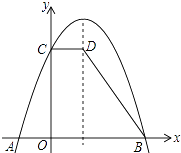

(1)、求该抛物线的解析式；

(2)、求梯形COBD的面积．

查看试题解析
21. 一个不透明的袋中装有5个黄球，13个黑球和22个红球，它们除颜色外都相同．

(1)、求从袋中摸出一个球是黄球的概率；

(2)、现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于 $\frac{1}{3}$ ，问至少取出了多少个黑球？

查看试题解析
22.
如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连接AC，CE．

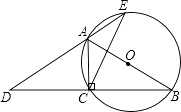(1)、求证：∠B=∠D；

(2)、若AB=4，BC﹣AC=2，求CE的长．

查看试题解析
23. 某校举办八年级学生数学素养大赛，比赛共设四个项目：七巧板拼图，趣题巧解，数学应用，魔方复原，每个项目得分都按一定百分比折算后记入总分，下表为甲，乙，丙三位同学得分情况（单位：分）

七巧板拼图
趣题巧解
数学应用
魔方复原
甲
66
89
86
68
乙
66
60
80
68
丙
66
80
90
68

(1)、比赛后，甲猜测七巧板拼图，趣题巧解，数学应用，魔方复原这四个项目得分分别按10%，40%，20%，30%折算记入总分，根据猜测，求出甲的总分；

(2)、本次大赛组委会最后决定，总分为80分以上（包含80分）的学生获一等奖，现获悉乙，丙的总分分别是70分，80分．甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分，问甲能否获得这次比赛的一等奖？

查看试题解析
24.
如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上的一动点，连接CD，DE，以CD，DE为边作▱CDEF．

(1)、当0＜m＜8时，求CE的长（用含m的代数式表示）；

(2)、当m=3时，是否存在点D，使▱CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；

(3)、点D在整个运动过程中，若存在唯一的位置，使得▱CDEF为矩形，请求出所有满足条件的m的值．

查看试题解析

	七巧板拼图	趣题巧解	数学应用	魔方复原
甲	66	89	86	68
乙	66	60	80	68
丙	66	80	90	68