2016-2017学年江西省宜春市七年级上学期期末数学试卷
试卷更新日期:2017-04-24 类型:期末考试
一、选择
-
1. 如果公司盈利20万元记作+20万元,那么亏本50万元记作( )A、+50万元 B、﹣50万元 C、+20万元 D、﹣20万元2. 下列计算正确的是( )A、3a+2a=5a2 B、4x﹣3x=1 C、3x2y﹣2yx2=x2y D、3a+2b=5ab3. 下列方程中变形正确的是( )
①4x+8=0变形为x+2=0;
②x+6=5﹣2x变形为3x=﹣1;
③ =3变形为4x=15;
④4x=2变形为x=2.
A、①④ B、①②③ C、③④ D、①②④4. 下列图形经过折叠不能围成棱柱的是( )A、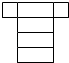 B、
B、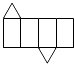 C、
C、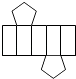 D、
D、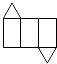 5. 我国古代名著《九章算术》中有一题“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”(凫:野鸭)设野鸭大雁与从北海和南海同时起飞,经过x天相遇,可列方程为( )A、(9﹣7)x=1 B、(9+7)x=1 C、( ﹣ )x=1 D、( + )x=16.
5. 我国古代名著《九章算术》中有一题“今有凫起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”(凫:野鸭)设野鸭大雁与从北海和南海同时起飞,经过x天相遇,可列方程为( )A、(9﹣7)x=1 B、(9+7)x=1 C、( ﹣ )x=1 D、( + )x=16.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是( )
 A、M=mn B、M=m(n+1) C、M=mn+1 D、M=n(m+1)
A、M=mn B、M=m(n+1) C、M=mn+1 D、M=n(m+1)二、填空题
-
7. 请你写出一个只含有字母m、n,且它的系数为﹣2、次数为3的单项式 .8. 2017年铁路春运预计发送旅客3.56亿人次,数据3.56亿用科学记数法表示为 .9. 当x=时,代数式4x﹣5与3x﹣9的值互为相反数.10. 如果代数式2x2+3x+7的值为8,那么代数式4x2+6x﹣9的值是 .11. 自习课时,同学抬头看见挂在黑板上方的时钟显示为9:30,此时时针与分针的夹角是度.12. 如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a﹣c|﹣|b﹣c|= .
 13. 下列说法中,
13. 下列说法中,①两点确定一条直线;
②两点之间,线段最短;
③连接两点的线段叫做这两点间的距离;
④同角(等角)的补角相等.
正确的有(只填序号).
14. 若线段AB的长度为6cm,线段BC的长度为4cm,A、B、C三点在同一直线上,且M为AB的中点,N为BC的中点,则线段MN的长度为 .三、解答题。
-
15. 计算(1)、计算:﹣7+(20﹣3)(2)、化简:3a﹣2b+4c﹣2a﹣6c+b.16. 解方程: .17. 先化简,再求值:﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中 a=﹣1,b=﹣2.18. 已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.
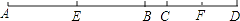 19. 用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a.
19. 用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a.如:1⊕3=1×32+2×1×3+1=16.
(1)、求(﹣2)⊕3的值;(2)、若( ⊕3)⊕(﹣ )=8,求a的值.20. 数学活动课上,小聪同学摆弄着自己刚购买的一套三角板,将两块直角三角板的直角顶点C叠放在一起,然后转动三角板,在转动过程中,请解决以下问题: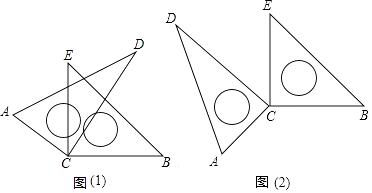 (1)、如图(1):当∠DCE=30°时,∠ACB+∠DCE等于多少?若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.(2)、当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.21. 在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
(1)、如图(1):当∠DCE=30°时,∠ACB+∠DCE等于多少?若∠DCE为任意锐角时,你还能求出∠ACB与∠DCE的数量关系吗?若能,请求出;若不能,请说明理由.(2)、当转动到图(2)情况时,∠ACB与∠DCE有怎样的数量关系?请说明理由.21. 在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米. (1)、若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;(2)、观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;(3)、现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.两队合作施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?22. 如图,点A、B都在数轴上,且AB=6
(1)、若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;(2)、观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;(3)、现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.两队合作施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?22. 如图,点A、B都在数轴上,且AB=6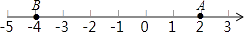 (1)、点B表示的数是;(2)、若点B以每秒2个单位的速度沿数轴向右运动,则2秒后点B表示的数是;(3)、若点A、B都以每秒2个单位沿数轴向右运动,而点O不动,t秒后有一个点是一条线段的中点,求t.
(1)、点B表示的数是;(2)、若点B以每秒2个单位的速度沿数轴向右运动,则2秒后点B表示的数是;(3)、若点A、B都以每秒2个单位沿数轴向右运动,而点O不动,t秒后有一个点是一条线段的中点,求t.