2013年浙江省衢州市中考数学试卷
试卷更新日期:2017-04-24 类型:中考真卷
一、选择题
-
1. 比1小2的数是( )A、3 B、1 C、﹣1 D、﹣22. 下列计算正确的是( )A、3a+2b=5ab B、a•a4=a4 C、a6÷a2=a3 D、(﹣a3b)2=a6b23. 衢州新闻网2月16日讯,2013年春节“黄金周”全市接待游客总数为833100人次.将数833100用科学记数法表示应为( )A、0.833×106 B、83.31×105 C、8.331×105 D、8.331×1044. 下面简单几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 若函数y= 的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )A、m<﹣2 B、m<0 C、m>﹣2 D、m>06. 将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
5. 若函数y= 的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )A、m<﹣2 B、m<0 C、m>﹣2 D、m>06. 将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )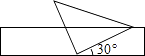 A、3cm B、6cm C、 cm D、 cm7. 一次数学测试,某小组五名同学的成绩如表所示(有两个数据被遮盖).
A、3cm B、6cm C、 cm D、 cm7. 一次数学测试,某小组五名同学的成绩如表所示(有两个数据被遮盖).组员
甲
乙
丙
丁
戊
方差
平均成绩
得分
81
79
■
80
82
■
80
那么被遮盖的两个数据依次是( )
A、80,2 B、80, C、78,2 D、78,8.如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高(AB)为1.6m,则这棵树的高度为( )(结果精确到0.1m, ≈1.73).
 A、3.5m B、3.6m C、4.3m D、5.1m9. 抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x﹣1)2﹣4,则b、c的值为( )A、b=2,c=﹣6 B、b=2,c=0 C、b=﹣6,c=8 D、b=﹣6,c=210.
A、3.5m B、3.6m C、4.3m D、5.1m9. 抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x﹣1)2﹣4,则b、c的值为( )A、b=2,c=﹣6 B、b=2,c=0 C、b=﹣6,c=8 D、b=﹣6,c=210.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A 的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
 A、
A、 B、
B、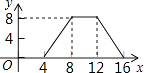 C、
C、 D、
D、
二、填空题
-
11. 不等式组 的解集是 .12. 化简: = .13. 小芳同学有两根长度为4cm、10cm的木棒,她想钉一个三角形相框,桌上有五根木棒供她选择(如图所示),从中任选一根,能钉成三角形相框的概率是 .
 14. 如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 .
14. 如图,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧( )对应的圆心角(∠AOB)为120°,OC的长为2cm,则三角板和量角器重叠部分的面积为 . 15. 某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种棵橘子树,橘子总个数最多.16. 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是 .
15. 某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一棵树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种棵橘子树,橘子总个数最多.16. 如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是;四边形A2013B2013C2013D2013的周长是 .
三、简答题
-
17. ﹣23÷|﹣2|×(﹣7+5)18. 如图所示,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
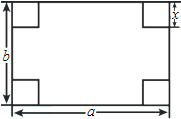 (1)、用a,b,x表示纸片剩余部分的面积;(2)、当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.19. 如图,函数y1=﹣x+4的图象与函数y2= (x>0)的图象交于A(a,1)、B(1,b)两点.
(1)、用a,b,x表示纸片剩余部分的面积;(2)、当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.19. 如图,函数y1=﹣x+4的图象与函数y2= (x>0)的图象交于A(a,1)、B(1,b)两点. (1)、求函数y2的表达式;(2)、观察图象,比较当x>0时,y1与y2的大小.20. 如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
(1)、求函数y2的表达式;(2)、观察图象,比较当x>0时,y1与y2的大小.20. 如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E. (1)、求证:直线CD是⊙O的切线;(2)、若DE=2BC,求AD:OC的值.21. 据《2012年衢州市国民经济和社会发展统计公报》(2013年2月5日发布),衢州市固定资产投资的相关数据统计图如下:
(1)、求证:直线CD是⊙O的切线;(2)、若DE=2BC,求AD:OC的值.21. 据《2012年衢州市国民经济和社会发展统计公报》(2013年2月5日发布),衢州市固定资产投资的相关数据统计图如下:
根据以上信息,解答下列问题:
(1)、求2012年的固定资产投资增长速度(年增长速度即年增长率);(2)、求2005﹣2012年固定资产投资增长速度这组数据的中位数;(3)、求2006年的固定资产投资金额,并补全条形图;(4)、如果按照2012年的增长速度,请预测2013年衢州市的固定资产投资金额可达到多少亿元(精确到1亿元)?22. (1)、【提出问题】
(1)、【提出问题】如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
(2)、【类比探究】如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)、【拓展延伸】如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
23.“五•一”假期,某火车客运站旅客流量不断增大,旅客往往需要长时间排队等候检票.经调查发现,在车站开始检票时,有640人排队检票.检票开始后,仍有旅客继续前来排队检票进站.设旅客按固定的速度增加,检票口检票的速度也是固定的.检票时,每分钟候车室新增排队检票进站16人,每分钟每个检票口检票14人.已知检票的前a分钟只开放了两个检票口.某一天候车室排队等候检票的人数y(人)与检票时间x(分钟)的关系如图所示.
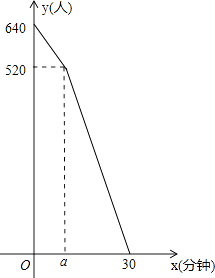 (1)、求a的值.(2)、求检票到第20分钟时,候车室排队等候检票的旅客人数.(3)、若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?24.
(1)、求a的值.(2)、求检票到第20分钟时,候车室排队等候检票的旅客人数.(3)、若要在开始检票后15分钟内让所有排队的旅客都能检票进站,以便后来到站的旅客随到随检,问检票一开始至少需要同时开放几个检票口?24.在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
 (1)、当点P移动到点D时,求出此时t的值;(2)、当t为何值时,△PQB为直角三角形;(3)、已知过O、P、Q三点的抛物线解析式为y=﹣ (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(1)、当点P移动到点D时,求出此时t的值;(2)、当t为何值时,△PQB为直角三角形;(3)、已知过O、P、Q三点的抛物线解析式为y=﹣ (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.