2013年浙江省宁波市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣5的绝对值为（）

A、﹣5 B、5 C、﹣ $\frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 下列计算正确的是（）

A、a²+a²=a⁴ B、2a﹣a=2 C、（ab）²=a²b² D、（a²）³=a⁵

查看试题解析
3. 下列电视台的台标，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 在一个不透明的布袋中装有3个白球和5个红球，它们除了颜色不同外，其余均相同．从中随机摸出一个球，摸到红球的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{3}$ C、 $\frac{3}{8}$ D、 $\frac{5}{8}$

查看试题解析
5. 备受宁波市民关注的象山港跨海大桥在2012年12月29日建成通车，此项目总投资约77亿元，77亿元用科学记数法表示为（）

A、7.7×10⁹元 B、7.7×10¹⁰元 C、0.77×10¹⁰元 D、0.77×10¹¹元

查看试题解析
6. 一个多边形的每个外角都等于72°，则这个多边形的边数为（）

A、5 B、6 C、7 D、8

查看试题解析
7. 两个圆的半径分别为2和3，当圆心距d=5时，这两个圆的位置关系是（）

A、内含 B、内切 C、相交 D、外切

查看试题解析
8. 如果三角形的两条边分别为4和6，那么连结该三角形三边中点所得的周长可能是下列数据中的（）

A、6 B、8 C、10 D、12

查看试题解析
9. 下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方体包装盒的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，二次函数y=ax²+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0），下列结论中，正确的一项是（）

A、abc＜0 B、2a+b＜0 C、a﹣b+c＜0 D、4ac﹣b²＜0

查看试题解析
11. 如图，梯形ABCD中，AD∥BC，AB= $\frac{5}{2}$ ，BC=4，连结BD，∠BAD的平分线交BD于点E，且AE∥CD，则AD的长为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{2}$ C、 $\frac{5}{3}$ D、2

查看试题解析
12. 7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）

A、a= $\frac{5}{2}$ b B、a=3b C、a= $\frac{7}{2}$ b D、a=4b

查看试题解析

二、填空题

13. 实数﹣8的立方根是．

查看试题解析
14. 分解因式：x²﹣4= ．

查看试题解析
15. 已知一个函数的图象与y= $\frac{6}{x}$ 的图象关于y轴成轴对称，则该函数的解析式为．

查看试题解析
16. 数据﹣2，﹣1，0，3，5的方差是．

查看试题解析
17. 如图，AE是半圆O的直径，弦AB=BC=4 $\sqrt{2}$ ，弦CD=DE=4，连结OB，OD，则图中两个阴影部分的面积和为．

查看试题解析
18. 如图，等腰直角三角形ABC顶点A在x轴上，∠BCA=90°，AC=BC=2 $\sqrt{2}$ ，反比例函数y= $\frac{3}{x}$ （x＞0）的图象分别与AB，BC交于点D，E．连结DE，当△BDE∽△BCA时，点E的坐标为．

查看试题解析

三、解答题

19. 先化简，再求值：（1+a）（1﹣a）+（a﹣2）² ，其中a=﹣3．

查看试题解析
20. 解方程： $\frac{3}{1 - x}$ = $\frac{x}{x - 1}$ ﹣5．

查看试题解析
21.
天封塔历史悠久，是宁波著名的文化古迹．如图，从位于天封塔的观测点C测得两建筑物底部A，B的俯角分别为45°和60°，若此观测点离地面的高度为51米，A，B两点在CD的两侧，且点A，D，B在同一水平直线上，求A，B之间的距离（结果保留根号）

查看试题解析
22. 2013年5月7日浙江省11个城市的空气质量指数（AQI）如图所示：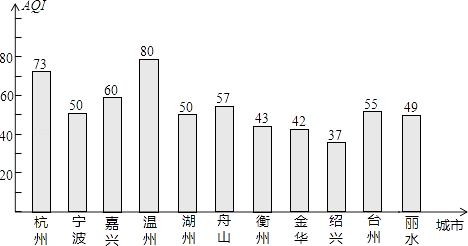

(1)、这11个城市当天的空气质量指数的极差、众数和中位数分别是多少？

(2)、当0≤AQI≤50时，空气质量为优．求这11个城市当天的空气质量为优的频率；

(3)、求宁波、嘉兴、舟山、绍兴、台州五个城市当天的空气质量指数的平均数．

查看试题解析
23. 已知抛物线y=ax²+bx+c与x轴交于点A（1，0），B（3，0），且过点C（0，﹣3）．

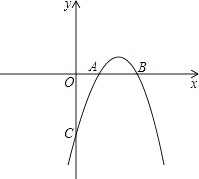(1)、求抛物线的解析式和顶点坐标；

(2)、请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=﹣x上，并写出平移后抛物线的解析式．

查看试题解析
24. 某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表：

甲
乙
进价（元/部）
4000
2500
售价（元/部）
4300
3000
该商场计划购进两种手机若干部，共需15.5万元，预计全部销售后可获毛利润共2.1万元．
（毛利润=（售价﹣进价）×销售量）

(1)、该商场计划购进甲、乙两种手机各多少部？

(2)、通过市场调研，该商场决定在原计划的基础上，减少甲种手机的购进数量，增加乙种手机的购进数量．已知乙种手机增加的数量是甲种手机减少的数量的2倍，而且用于购进这两种手机的总资金不超过16万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润．

查看试题解析
25.
若一个四边形的一条对角线把四边形分成两个等腰三角形，我们把这条对角线叫这个四边形的和谐线，这个四边形叫做和谐四边形．如菱形就是和谐四边形．

(1)、如图1，在梯形ABCD中，AD∥BC，∠BAD=120°，∠C=75°，BD平分∠ABC．求证：BD是梯形ABCD的和谐线；

(2)、如图2，在12×16的网格图上（每个小正方形的边长为1）有一个扇形BAC，点A．B．C均在格点上，请在答题卷给出的两个网格图上各找一个点D，使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线，并画出相应的和谐四边形；

(3)、四边形ABCD中，AB=AD=BC，∠BAD=90°，AC是四边形ABCD的和谐线，求∠BCD的度数．

查看试题解析
26.
如图，在平面直角坐标系中，O为坐标原点，点A的坐标为（0，4），点B的坐标为（4，0），点C的坐标为（﹣4，0），点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P，D，B三点作⊙Q与y轴的另一个交点为E，延长DQ交⊙Q于点F，连结EF，BF．

(1)、求直线AB的函数解析式；

(2)、当点P在线段AB（不包括A，B两点）上时．
①求证：∠BDE=∠ADP；
②设DE=x，DF=y．请求出y关于x的函数解析式；

(3)、请你探究：点P在运动过程中，是否存在以B，D，F为顶点的直角三角形，满足两条直角边之比为2：1？如果存在，求出此时点P的坐标：如果不存在，请说明理由．

查看试题解析

	甲	乙
进价（元/部）	4000	2500
售价（元/部）	4300	3000