2012年浙江省舟山市中考数学试卷

试卷更新日期：2017-04-24 类型：中考真卷

进入出卷网下载

一、选择题

1. （﹣2）⁰等于（）

A、1 B、2 C、0 D、﹣2

查看试题解析
2. 下列图案中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 南海资源丰富，其面积约为350万平方千米，相当于我国的渤海、黄海和东海总面积的3倍．其中350万用科学记数法表示为（）

A、0.35×10⁸ B、3.5×10⁷ C、3.5×10⁶ D、35×10⁵

查看试题解析
4. 如图，AB是⊙0的弦，BC与⊙0相切于点B，连接OA、OB．若∠ABC=70°，则∠A等于（）

A、15° B、20° C、30° D、70°

查看试题解析
5. 若分式 $\frac{x - 1}{x + 2}$ 的值为0，则（）

A、x=﹣2 B、x=0 C、x=1或x=﹣2 D、x=1

查看试题解析
6. 如图，A、B两点在河的两岸，要测量这两点之间的距离，测量者在与A同侧的河岸边选定一点C，测出AC=a米，∠A=90°，∠C=40°，则AB等于（）米．

A、asin40° B、acos40° C、atan40° D、 $\frac{a}{\tan 40^{\circ}}$

查看试题解析
7. 已知一个圆锥的底面半径为3cm，母线长为10cm，则这个圆锥的侧面积为（）

A、15πcm² B、30πcm² C、60πcm² D、3 $\sqrt{91}$ cm²

查看试题解析
8. 定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”如“947”就是一个“V数”．若十位上的数字为2，则从1，3，4，5中任选两数，能与2组成“V数”的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{3}{10}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图，已知△ABC中，∠CAB=∠B=30°，AB=2 $\sqrt{3}$ ，点D在BC边上，把△ABC沿AD翻折使AB与AC重合，得△AB′D，则△ABC与△AB′D重叠部分的面积为（）

A、 $\frac{3 - \sqrt{3}}{2}$ B、 $\frac{\sqrt{3} - 1}{2}$ C、3﹣ $\sqrt{3}$ D、 $\frac{3 - \sqrt{3}}{6}$

查看试题解析
10. 如图，正方形ABCD的边长为a，动点P从点A出发，沿折线A→B→D→C→A的路径运动，回到点A时运动停止．设点P运动的路程长为x，AP长为y，则y关于x的函数图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 当a=2时，代数式3a﹣1的值是．

查看试题解析
12. 因式分解：a²﹣9= ．

查看试题解析
13. 在直角△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若CD=4，则点D到斜边AB的距离为．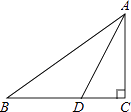

查看试题解析
14. 如图是嘉兴市某6天内的最高气温折线统计图，则最高气温的众数是℃．

查看试题解析
15. 如图，已知⊙O的半径为2，弦AB⊥半径OC，沿AB将弓形ACB翻折，使点C与圆心O重合，则月牙形（图中实线围成的部分）的面积是．

查看试题解析
16. 如图，在Rt△ABC中，AB=BC，∠ABC=90°，点D是AB的中点，连接CD，过点B作BG⊥CD，分别交CD，CA于点E，F，与过点A且垂直于AB的直线相交于点G，连接DF，给出以下五个结论：
① $\frac{A G}{A B} = \frac{F G}{F B}$ ；②∠ADF=∠CDB；③点F是GE的中点；④AF= $\frac{\sqrt{2}}{3}$ AB；⑤S_△_ABC=5S_△_BDF ，
其中正确结论的序号是．

查看试题解析

三、解答题

17. 计算：

(1)、丨﹣5|+ $\sqrt{16}$ ﹣3²

(2)、（x+1）²﹣x（x+2）

查看试题解析
18. 解不等式2（x﹣1）﹣3＜1，并把它的解集在数轴上表示出来．

查看试题解析
19. 如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连接CE．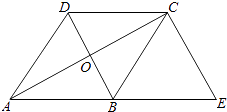

(1)、求证：BD=EC；

(2)、若∠E=50°，求∠BAO的大小．

查看试题解析
20. 为了解我市的空气质量情况，某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．
请你根据图中提供的信息，解答下列问题：

(1)、计算被抽取的天数；

(2)、请补全条形统计图，并求扇形统计图中表示“优”的扇形的圆心角度数；

(3)、请估计该市这一年（365天）达到“优”和“良”的总天数．

查看试题解析
21. 如图，一次函数y₁=kx+b的图象与反比例函数y₂= $\frac{m}{x}$ 的图象相交于点A（2，3）和点B，与x轴相交于点C（8，0）．

(1)、求这两个函数的解析式；

(2)、当x取何值时，y₁＞y₂ ．

查看试题解析
22. 某汽车租赁公司拥有20辆汽车．据统计，当每辆车的日租金为400元时，可全部租出；当每辆车的日租金每增加50元，未租出的车将增加1辆；公司平均每日的各项支出共4800元．设公司每日租出x辆车时，日收益为y元．（日收益=日租金收入一平均每日各项支出）

(1)、公司每日租出x辆车时，每辆车的日租金为元（用含x的代数式表示）；

(2)、当每日租出多少辆时，租赁公司日收益最大？最大是多少元？

(3)、当每日租出多少辆时，租赁公司的日收益不盈也不亏？

查看试题解析
23.
将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，即如图①，我们将这种变换记为[θ，n]．

(1)、如图①，对△ABC作变换[60°， $\sqrt{3}$ ]得△AB′C′，则S_△_AB′C′：S_△_ABC=；直线BC与直线B′C′所夹的锐角为度；

(2)、如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC 作变换[θ，n]得△AB′C′，使点B、C、C′在同一直线上，且四边形ABB'C'为矩形，求θ和n的值；

(3)、如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．

查看试题解析
24.
在平面直角坐标系xOy中，点P是抛物线：y=x²上的动点（点在第一象限内）．连接 OP，过点O作OP的垂线交抛物线于另一点Q．连接PQ，交y轴于点M．作PA丄x轴于点A，QB丄x轴于点B．设点P的横坐标为m．

(1)、如图1，当m= $\sqrt{2}$ 时，

①求线段OP的长和tan∠POM的值；

②在y轴上找一点C，使△OCQ是以OQ为腰的等腰三角形，求点C的坐标；

(2)、如图2，连接AM、BM，分别与OP、OQ相交于点D、E．
①用含m的代数式表示点Q的坐标；
②求证：四边形ODME是矩形．

查看试题解析