2018-2019学年人教版数学九年级下册 27.2.3相似三角形应用举例 同步练习
试卷更新日期:2019-03-09 类型:同步测试
一、选择题
-
1. 如图,要在宽为22米的九州大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,此时,路灯的灯柱BC高度应该设计为( )
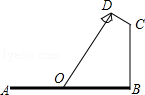 A、(11﹣2 )米 B、(11 ﹣2 )米 C、(11﹣2 )米 D、(11 ﹣4)米2. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )
A、(11﹣2 )米 B、(11 ﹣2 )米 C、(11﹣2 )米 D、(11 ﹣4)米2. 学校门口的栏杆如图所示,栏杆从水平位置 绕 点旋转到 位置,已知 , ,垂足分别为 , , , , ,则栏杆 端应下降的垂直距离 为( )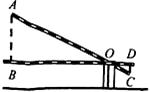 A、 B、 C、 D、3. 如图,小明在 时测得某树的影长为 , 时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为( )m.
A、 B、 C、 D、3. 如图,小明在 时测得某树的影长为 , 时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为( )m. A、2 B、4 C、6 D、84. 如图,在针孔成像问题中,根据图形尺寸可知像 的长是物AB长的( )
A、2 B、4 C、6 D、84. 如图,在针孔成像问题中,根据图形尺寸可知像 的长是物AB长的( )
A、3倍 B、不知AB的长度,无法计算 C、 D、5. 如图,小明为了测量一凉亭的高度AB(顶端A到水平地面BD的距离),在凉亭的旁边放置一个与凉亭台阶BC等高的台阶DE(DE=BC=0.5米,A、B、C三点共线),把一面镜子水平放置在平台上的点G处,测得CG=15米,然后沿直线CG后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得EG=3米,小明身高1.6米,则凉亭的高度AB约为( ) A、8.5米 B、9米 C、9.5米 D、10米6. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( )
A、8.5米 B、9米 C、9.5米 D、10米6. 为测量操场上旗杆的高度,小丽同学想到了物理学中平面镜成像的原理,她拿出随身携带的镜子和卷尺,先将镜子放在脚下的地面上,然后后退,直到她站直身子刚好能从镜子里看到旗杆的顶端E,标记好脚掌中心位置为B,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,如图所示.已知小丽同学的身高是1.54m,眼睛位置A距离小丽头顶的距离是4cm,则旗杆DE的高度等于( ) A、10m B、12m C、12.4m D、12.32m7. 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
A、10m B、12m C、12.4m D、12.32m7. 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )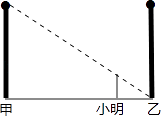 A、7米 B、8米 C、9米 D、10米8. 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( )
A、7米 B、8米 C、9米 D、10米8. 如图,为了估计荆河的宽度,在荆河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R,如果QS=60m,ST=120m,QR=80m,则荆河的宽度PQ为( ) A、40m B、120m C、60m D、180m9. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
A、40m B、120m C、60m D、180m9. 为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )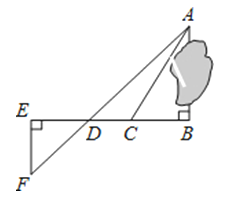 A、BC,∠ACB B、DE,DC,BC C、EF,DE,BD D、CD,∠ACB,∠ADB
A、BC,∠ACB B、DE,DC,BC C、EF,DE,BD D、CD,∠ACB,∠ADB二、填空题
-
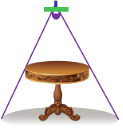
10. 如图,圆桌面正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形).已知灯泡距离地面2.4m,桌面距离地面0.8m(桌面厚度不计算),若桌面的面积是1.2m2 , 则地面上的阴影面积是 m2 .
 11.
11.综合实践课上,小宇设计用光学原理来测量公园假山的高度,把一面镜子放在与假山AC距离为21米的B处,然后沿着射线CB退后到点E,这时恰好在镜子里看到山头A,利用皮尺测量BE=2.1米.若小宇的身高是1.7米,则假山AC的高度为 .
 12. 现有一个测试距离为5m的视力表,根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的=
12. 现有一个测试距离为5m的视力表,根据这个视力表,小华想制作一个测试距离为3m的视力表,则图中的=
三、解答题
-
13. 我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路。
 14. 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)
14. 晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语塞.小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人在灯下沿直线NQ移动,如图,当小聪正好站在广场的A点(距N点5块地砖长)时,其影长AD恰好为1块地砖长;当小军正好站在广场的B点(距N点9块地砖长)时,其影长BF恰好为2块地砖长.已知广场地面由边长为0.8米的正方形地砖铺成,小聪的身高AC为1.6米,MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高BE的长.(结果精确到0.01米)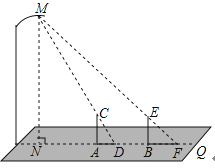 15. 如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1 , 然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m.
15. 如图,为测量学校围墙外直立电线杆AB的高度,小亮在操场上点C处直立高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小亮又在点C1处直立高3m的竹竿C1D1 , 然后退到点E1处,此时恰好看到竹竿顶端D1与电线杆顶端B重合.小亮的眼睛离地面高度EF=1.5m,量得CE=2m,EC1=6m,C1E1=3m.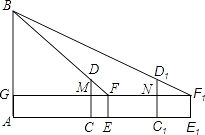 (1)、△FDM∽△ , △F1D1N∽△(2)、求电线杆AB的高度.
(1)、△FDM∽△ , △F1D1N∽△(2)、求电线杆AB的高度.

