2018-2019学年人教版数学九年级下册 27.2.2相似三角形的性质 同步练习
试卷更新日期:2019-03-09 类型:同步测试
一、选择题
-
1. 已知△ABC∽△DEF,AB的对应边是DE,且AB=4,DE=2,则△DEF的面积与△ABC的面积之比( )A、1:2 B、1:4 C、2:1 D、4:12. 已知△ABC~△DEF,S△ABC:S△DEF=9,且△ABC的周长为18,则△DEF的周长为( )A、2 B、3 C、6 D、543. 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
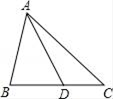 A、AB2=BC•BD B、AB2=AC•BD C、AB•AD=BD•BC D、AB•AD=AD•CD4. 已知△ABC∽△A′B′C′, ,AB边上的中线CD长4cm,△ABC的周长20cm,则△A′B′C′的周长和A′B′边上的中线C′D′分别长( )A、10cm,2cm B、40cm,8cm C、40cm,2cm D、10cm,8cm5. 两相似三角形对应高长的比为3:4,则对应中线长的比为( )A、3:4 B、9:16 C、 :2 D、4:36. 把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大( );若边长扩大5倍,则面积扩大( )A、5倍,10倍 B、10倍,25倍 C、 倍,25倍 D、25倍,25倍7. 相似三角形的最短边分别是5cm和3cm,它们的面积之差为 ,那么小三角形的面积为( )
A、AB2=BC•BD B、AB2=AC•BD C、AB•AD=BD•BC D、AB•AD=AD•CD4. 已知△ABC∽△A′B′C′, ,AB边上的中线CD长4cm,△ABC的周长20cm,则△A′B′C′的周长和A′B′边上的中线C′D′分别长( )A、10cm,2cm B、40cm,8cm C、40cm,2cm D、10cm,8cm5. 两相似三角形对应高长的比为3:4,则对应中线长的比为( )A、3:4 B、9:16 C、 :2 D、4:36. 把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大( );若边长扩大5倍,则面积扩大( )A、5倍,10倍 B、10倍,25倍 C、 倍,25倍 D、25倍,25倍7. 相似三角形的最短边分别是5cm和3cm,它们的面积之差为 ,那么小三角形的面积为( )
A、 B、 C、 D、8. 如图,DE∥BC,CD与BE相交于点O,若 ,则 的值为( ) A、 B、 C、
A、 B、 C、 D、
9. 已知两个相似三角形的周长比为2:3,它们的面积之差为 ,那么它们的面积之和为A、
D、
9. 已知两个相似三角形的周长比为2:3,它们的面积之差为 ,那么它们的面积之和为A、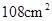 B、
B、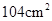 C、
C、 D、
D、
二、填空题
-
10. 已知△ABC∽△DEF,且相似比为3:4,S△ABC=2cm2 , 则S△DEF=11. 如图,DE是△ABC的中位线,若△ADE的面积为3,则△ABC的面积为 .
 12. 如果两个相似三角形周长的比是 ,那么它们面积的比是 .13. 经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形 △CBD和△ABC相似,∠A =46°,则 ∠ACB的度数为 .
12. 如果两个相似三角形周长的比是 ,那么它们面积的比是 .13. 经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形 △CBD和△ABC相似,∠A =46°,则 ∠ACB的度数为 .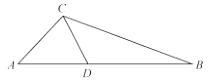 14. △ABC的3条边的长分别为6、8、10,与其相似的△DEF的最长边为15,则△DEF的最短边为 , △DEF的面积为 .15. 在△ABC中,AB=9,AC=12,BC=18,D是AC边上一点,DC= AC,在AB边上取一点E,连接DE,若两个三角形相似,则DE的长为 .
14. △ABC的3条边的长分别为6、8、10,与其相似的△DEF的最长边为15,则△DEF的最短边为 , △DEF的面积为 .15. 在△ABC中,AB=9,AC=12,BC=18,D是AC边上一点,DC= AC,在AB边上取一点E,连接DE,若两个三角形相似,则DE的长为 .三、解答题
-
16. 如图,已知△ABC∽△AED,AD=5cm,AC=10cm,AE=6cm,∠A=66°,∠ADE=65°,求AB的长及∠C的度数.
 17. 如图,已知以点A、D、E为顶点的三角形与△ABC相似,且AD=3,DE=2.5,AE=4,AC=6,∠AED=∠B,求△ABC的周长.
17. 如图,已知以点A、D、E为顶点的三角形与△ABC相似,且AD=3,DE=2.5,AE=4,AC=6,∠AED=∠B,求△ABC的周长. 18. 如图,在矩形ABCD中,AB=3cm,AD=4cm,点E是BC上一动点(不与B、C重合),且DF⊥AE,垂足为F. 设AE=xcm,DF=ycm.
18. 如图,在矩形ABCD中,AB=3cm,AD=4cm,点E是BC上一动点(不与B、C重合),且DF⊥AE,垂足为F. 设AE=xcm,DF=ycm.
(1)求证:△DFA∽△ABE;
(2)试求y与x之间的函数关系式,并求出自变量x的取值范围.

