四川省绵阳市2018-2019学年高三理数第二次（1月)诊断性考试试卷

试卷更新日期：2019-03-08 类型：高考模拟

进入出卷网下载

一、单选题

1. 在复平面内，复数 $\frac{1}{2 + i}$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知集合A={0， 1，2， 3，4}，B=｜x ｜ $e^{x - 1}$ ＞1｝，则A∩B＝（）

A、{1，2，3，4} B、{2，3，4} C、{3，4} D、{4}

查看试题解析
3. 下图所示的茎叶图记录的是甲、乙两个班各5名同学在一次数学小测试中的选择题总成绩（每道题5分，共8道题）．已知两组数据的中位数相同，则m的值为（）

A、0 B、2 C、3 D、5

查看试题解析
4. “a＝b＝1”是“直线ax－y+1＝0与直线x－by－1＝0平行”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
5. 设 $a, b$ 是互相垂直的单位向量，且（ $λ a$ ＋ $b$ ）⊥（ $a$ ＋2 $b$ ），则实数 $λ$ 的值是（）

A、2 B、－2 C、1 D、－1

查看试题解析
6. 执行如图的程序框图，其中输入的 $a = sin \frac{7 π}{6}$ ， $b = cos \frac{7 π}{6}$ ，则输出a的值为（）

A、－1 B、1 C、 $\sqrt{3}$ D、－ $\sqrt{3}$

查看试题解析
7. 抛物线 $y^{2} = 4 \sqrt{2} x$ 的焦点为F，P是抛物线上一点，过P作y轴的垂线，垂足为Q，若｜PF｜＝ $4 \sqrt{2}$ ，则△PQF的面积为（）

A、3 B、 C、 D、 $6 \sqrt{3}$

查看试题解析
8. 已知⊙O： $x^{2} + y^{2} = 5$ 与⊙O₁： ${(x - a)}^{2} + y^{2} = r^{2} (a > 0)$ 相交于A、B两点，若两圆在A点处的切线互相垂直，且｜AB｜=4，则⊙O₁的方程为（）

A、＝20 B、＝50 C、＝20 D、＝50

查看试题解析
9. 在边长为2的等边三角形内随机取一点，该点到三角形三个顶点距离均大于1的概率是（）

A、 B、 C、 D、

查看试题解析
10. 已知F₁ ， F₂是焦距为8的双曲线E： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点，点F₂关于双曲线E的一条渐近线的对称点为点A，若｜AF₁｜＝4，则此双曲线的离心率为（）

A、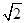 B、 $\sqrt{3}$ C、2 D、3

查看试题解析
11. 博览会安排了分别标有序号为“1号”“2号”“3号”的三辆车，等可能随机顺序前往酒店接嘉宾．某嘉宾突发奇想，设计两种乘车方案．方案一：不乘坐第一辆车，若第二辆车的车序号大于第一辆车的车序号，就乘坐此车，否则乘坐第三辆车；方案二：直接乘坐第一辆车．记方案一与方案二坐到“3号”车的概率分别为P₁ ， P₂ ，则（）

A、P₁•P₂＝ $\frac{1}{4}$ B、P₁＝P₂＝ C、P₁+P₂＝ $\frac{5}{6}$ D、P₁＜P₂

查看试题解析
12. 函数 $f (x) = e^{x - 1} - \frac{1}{2} a x^{2} + (a - 1) x + a^{2}$ 在（一∞，十∞）上单调递增，则实数a的范围是（）

A、{1} B、(－1，1) C、(0. 1) D、{－1，1}

查看试题解析

二、填空题

13. (2+ $\frac{1}{x}$ )(2＋x)⁵的展开式中x²的系数是． (用数字作答）

查看试题解析
14. 一个盒子装有3个红球和2个蓝球（小球除颜色外其它均相同），从盒子中一次性随机取出3个小球后，再将小球放回．重复50次这样的实验．记“取出的3个小球中有2个红球，1个蓝球”发生的次数为 $ξ$ ，则 $ξ$ 的方差是．

查看试题解析
15. 若f（x)＝ $e^{x} - e^{- x}$ ，则满足不等式f(3x一1)十f(2)＞0的x的取值范围是．

查看试题解析
16. 已知椭圆C： $\frac{x^{2}}{m} + \frac{y^{2}}{m - 4} = 1 (m > 4)$ 的右焦点为F，点A（一2，2)为椭圆C内一点。若椭圆C上存在一点P，使得｜PA｜＋｜PF｜＝8，则m的最大值是．

查看试题解析

三、解答题

17. 设数列｛ $a_{n}$ ｝的前n项和为Sn，已知3Sn=4 $a_{n}$ －4， $n \in N *$ ．

(1)、求数列｛ $a_{n}$ ｝的通项公式；

(2)、令 $b_{n} = \frac{1}{{log}_{2} a_{n} \cdot {log}_{2} a_{n + 1}}$ ，求数列｛ $b_{n}$ ｝的前n项和Tn.

查看试题解析
18. 进入冬天，大气流动性变差，容易形成雾握天气，从而影响空气质量．某城市环保部门试图探究车流量与空气质量的相关性，以确定是否对车辆实施限行．为此，环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表：

注：回归方程 $\hat{y} = \hat{b} x + \hat{a}$ 中斜率和截距最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} ， \hat{a} = \bar{y} - \hat{b} \bar{x}$ .

(1)、根据表中周一到周五的数据，求y关于x的线性回归方程。

(2)、若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2，则认为得到的线性回归方程是可靠的．请根据周六和周日数据，判定所得的线性回归方程是否可靠？

查看试题解析
19. △ABC的内角A．B．C的对边分别为a，b，c，已知 $\sqrt{3} \overset{⇀}{A B} \cdot \overset{⇀}{A C}$ ＝b（c－asinC）。

(1)、求角A的大小；

(2)、设b=c，N是△ABC所在平面上一点，且与A点分别位于直线BC的两侧，如图，若BN=4，CN=2，求四边形ABNC面积的最大值．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{8} + \frac{y^{2}}{4} = 1$ 的左右焦点分别为F₁ ， F₂ ，直线l：y＝kx+m与椭圆C交于A，B两点．O为坐标原点．

(1)、若直线l过点F₁ ，且｜AF₂｜十｜BF₂ ｜＝ $\frac{16 \sqrt{2}}{3}$ ，求直线l的方程；

(2)、若以AB为直径的圆过点O，点P是线段AB上的点，满足OP⊥AB，求点P的轨迹方程．

查看试题解析
21. 已知函数 $f (x) = x ln x - \frac{1}{2} m x^{2} - x + 1 ， m \in R$ .

(1)、若f（x）有两个极值点，求实数m的取值范围：

(2)、若函数 $g (x) = x ln x - m x^{2} - e ln x + e m x$ 有且只有三个不同的零点，分别记为x₁ ， x₂ ， x₃ ，设x₁＜x₂＜x₃ ，且 $\frac{x_{3}}{x_{1}}$ 的最大值是e² ，求x₁x₃的最大值．

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程是 ${\begin{matrix} x = 2 + 3 c o s θ \\ y = 3 s i n θ \end{matrix}$ （θ为参数）．以坐标原点O为极点，x轴正半轴为极轴，建立极坐标系，直线l的极坐标方程为： $ρ (cos θ + sin θ) = t$

(1)、求曲线C的极坐标方程；

(2)、设直线θ＝ $\frac{π}{6} (ρ \in R)$ 与直线l交于点M，与曲线C交于P，Q两点，已知｜OM｜•｜OP｜•｜OQ）＝10，求t的值。

查看试题解析
23. 已知函数 $f (x) = | x - m |, m \in R$

(1)、m＝1时，求不等式f（x－2）+f（2x）＞4的解集；

(2)、若t＜0，求证： $f (t x)$ ≥ $t f (x) + f (t m)$ ．

查看试题解析