浙江省金华市2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 下列各组数中互为相反数的是( )A、-2与-
 B、-5与
B、-5与  C、-3与
C、-3与 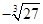 D、|-6|与-6
2. 在 ,3.14,0, 中,属于分数的是( )A、
D、|-6|与-6
2. 在 ,3.14,0, 中,属于分数的是( )A、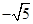 B、3.14
C、0
D、
3. 下列计算正确的是( )A、5m-2n=3 B、6x3+4x7=10x10 C、3a+2a=5a2 D、8a2b-8ba2=04. 有下面的算式:①(-1)2001=-2001;②0-(-1)=1;③ ;④2×(-3)2=-12;⑤-3÷ ×2=-3;⑥ =±4,正确的有( )个A、1 B、2 C、3 D、4-5. 若A和B都是六次多项式,则A+B一定是( )A、六次多项式 B、十二次多项式 C、不高于六次的整式 D、单项式6. 对于有理数x, 的值是( )A、0 B、2018 C、
B、3.14
C、0
D、
3. 下列计算正确的是( )A、5m-2n=3 B、6x3+4x7=10x10 C、3a+2a=5a2 D、8a2b-8ba2=04. 有下面的算式:①(-1)2001=-2001;②0-(-1)=1;③ ;④2×(-3)2=-12;⑤-3÷ ×2=-3;⑥ =±4,正确的有( )个A、1 B、2 C、3 D、4-5. 若A和B都是六次多项式,则A+B一定是( )A、六次多项式 B、十二次多项式 C、不高于六次的整式 D、单项式6. 对于有理数x, 的值是( )A、0 B、2018 C、 D、
D、 7. 某同学从家里到学校时,每小时行5千米;按原路返回家时,每小时行4千米,返回的时间比去学校的时间多花10分钟.设去学校所用的时间为x小时,则可列方程为( )A、
7. 某同学从家里到学校时,每小时行5千米;按原路返回家时,每小时行4千米,返回的时间比去学校的时间多花10分钟.设去学校所用的时间为x小时,则可列方程为( )A、 B、
B、 C、
C、 D、
D、 8. 下列说法正确的是( )A、两点之间的距离是两点间的线段 B、已知∠1+∠2+∠3=180°,则∠1,∠2,∠3互补 C、同一平面内,过一点有且只有一条直线与已知直线垂直 D、与同一条直线垂直的两条直线也垂直9. 如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )
8. 下列说法正确的是( )A、两点之间的距离是两点间的线段 B、已知∠1+∠2+∠3=180°,则∠1,∠2,∠3互补 C、同一平面内,过一点有且只有一条直线与已知直线垂直 D、与同一条直线垂直的两条直线也垂直9. 如图,直线AB、CD相交于点E,EF⊥AB于E,若∠CEF=59°,则∠AED的度数为( )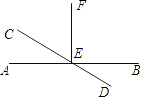 A、149° B、121° C、95° D、31°10. 两个形状大小完全相同的长方形中放入4个相同的小长方形后,得到图①和图②的阴影部分,如果大长方形的长为a,则图①与图②的阴影部分周长之差是( )
A、149° B、121° C、95° D、31°10. 两个形状大小完全相同的长方形中放入4个相同的小长方形后,得到图①和图②的阴影部分,如果大长方形的长为a,则图①与图②的阴影部分周长之差是( )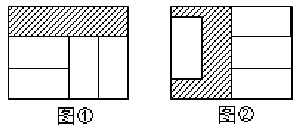 A、 B、
A、 B、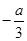 C、
C、 D、
D、
二、填空题
-
11. 近年来国家重视精准扶贫收效显著,据统计约65000000人脱贫,65000000用科学记数法表示为.12. 已知方程3(2x-1)=1-2x与关于x的方程8-k=2(x+1)的解相同,则k=.13. ∠α的补角是140°15’13”,则∠α的余角是.14. 如图,已知AB=5,点C在直线AB上,且BC=4,M为BC的中点,则线段AM的长度为.
 15. 已知f(x)= ,其中f(a)表示当x=a时对应的代数式的值,如f(0)= ,则
15. 已知f(x)= ,其中f(a)表示当x=a时对应的代数式的值,如f(0)= ,则f( )+f( )+f( )+…+f( )+f(1)+f(0)+f(1)+f(2)+…+f(2016)+f(2017)+f(2018)=.
16. 设 , , , ,设 ,则计算后 =.三、解答题
-
17. 计算:(1)、28+(-31)-(-13)(2)、-22+ ÷(-2)×(3)、180°-(38°45’+72.5°)(结果用度、分、秒表示)18.(1)、先化简再求值: ,其中x=2,y=3.(2)、有两个多项式:A=2a2-4a+1,B=2(a2-2a)+3,当a取任意数时,请比较A与B的大小.
19. 解方程:(1)、4x-3(20-2x)=10(2)、20. 出租车司机小张某大上午营运全是在东西走向的大道上进行的,如果规定向东为正,向西为负,他这大上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)、将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?(2)、若汽车耗油量为0.6升/千米,出车时,油箱有油72升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天下午是否需要加油?料要加油至少需要加多少才能返回出发地?若不用加油,请说明理由.
21. 如图,直线AB、CD相交于点O,OE平分∠AOD. (1)、若∠AOC=46°,求∠DOE的度数;(2)、若∠DOE=2∠AOC+10°,求∠AOC,∠DOE的度数.22. 已知数轴上点A、B、C所表示的数分别是-3,+5,x.(1)、请在数轴上标出A、B两点;
(1)、若∠AOC=46°,求∠DOE的度数;(2)、若∠DOE=2∠AOC+10°,求∠AOC,∠DOE的度数.22. 已知数轴上点A、B、C所表示的数分别是-3,+5,x.(1)、请在数轴上标出A、B两点; (2)、若AC=2,求x的值;
(2)、若AC=2,求x的值;
(3)、求线段AB的中点D所表示的数;(4)、若x<0,用含x的代数式表示线段AC与线段BC的长度和.23. 如图是某市民健身广场的平面的示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米. (1)、设图中最大正方形B的边长是x米,请用含x的代数式表示出正方形F、E和C的边长,分别为多少米?
(1)、设图中最大正方形B的边长是x米,请用含x的代数式表示出正方形F、E和C的边长,分别为多少米?
(2)、求出x的值;(3)、现沿着长方形广场的四条边铺设下水管道,由甲、乙工程队单独铺设分别需要8天、10天完成.如果两队从同一点开始,沿相反的方向同时施上4天后,由甲队有任务,余下的工程由乙队单独施工,试问还要多少天完成?
24. 如图,线段AB=10,动点P从点A出发,以每秒1个单位的速度,沿线段AB向终点B运动,同时,另一个动点Q从点B出发,以每秒3个单位的速度在线段AB上来回运动(从点B向点A运动,到达点A后,立即原速返回,再次到达B点后立即调头向点A运动.)当点P到达B点时,P,Q两点都停止运动.设点P的运动时间为x. (1)、当x=3时,线段PQ的长为.(2)、当P,Q两点第一次重合时,求线段BQ的长.(3)、是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由。
(1)、当x=3时,线段PQ的长为.(2)、当P,Q两点第一次重合时,求线段BQ的长.(3)、是否存在某一时刻,使点Q恰好落在线段AP的中点上?若存在,请求出所有满足条件的x的值;若不存在,请说明理由。