广西河池市凤山县2019届九年级上学期数学期末考试试卷
试卷更新日期：2019-03-06 类型：期末考试
一、选择题
-
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列方程是一元二次方程的是（ ）A、x-2=0 B、x2-4x-1=0 C、x3-2x-3=0 D、xy+1=03. 下列事件中，是必然事件的是（ ）A、明天太阳从东方升起 B、打开电视机，正在播放体育新闻 C、射击运动员射击一次，命中靶心 D、经过有交通信号灯的路灯，遇到红灯4. 如图，点A，B，C都在⊙O上，若∠C=35°，则∠AOB的度数为（ ）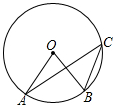
A、35° B、55° C、145° D、70°5. 抛物线y=2(x-1)2+3的对称轴为（ ）A、直线x=1 B、直线y=1 C、直线y=-1 D、直线x=-16. 在平面直角坐标系中，点P(1，2)关于x轴对称的点的坐标是（ ）A、(-1，-2) B、(-1，2) C、(1，-2) D、(2，1)7. 如图，已知△ABC中，AB=2，BC=3，∠B=90°，以点B为圆心作半径为r的⊙B，要使点A、C在⊙B外，则r的取值范围是（ ）
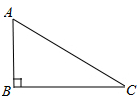A、0<r<2 B、0<r<3 C、2<r<3 D、r>38. 关于x的方程x2-2x+m=0有两个相等的实数根，则实数m的取值范围为（ ）A、m≥1 B、m<1 C、m=1 D、m<-19. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=6，BE=1，则弦CD的长是（ ）
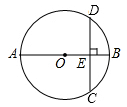A、4 B、5 C、
D、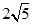
10. 方程2x2-7x+5=0的根的情况是（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、两根异号11. 如图，点A、B、C是圆O上的三点，且四边形OABC是平行四边形，OD⊥AB交圆O于点D，则∠OAD等于（ ）
A、72.5° B、75° C、80° D、60°12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，给出下列四个结论：①ac<0；②方程ax2+bx+c=0的两根是x1=1，x2=3；③b=2a；④函数的最大值是c-a．其中正确的是（ ）
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
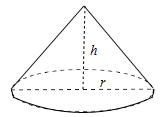
13. 关于x的一元二次方程(m-1)x2+x+m2-1=0有一根为0，则m的值为14. 将抛物线y=-x2+1向左平移2个单位长度，所得新抛物线的函数解析式为15. 将一副扑克牌中的13张梅花牌洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的牌上的数小于8的概率是16. 某工程一月份的产值为60万元，三月份的产值达到了72万元，设每月产值的增长率x相同，则可列出方程为17. 如图，圆锥的底面半径r为6，高h为8，则圆锥的侧面展开图扇形的圆心角为
18. 如图，在Rt△ABC中，∠ABC=90°，AB=BC=4，将△ABC绕点A顺时针旋转60°，得到△ADE，连结BE，则BE的长为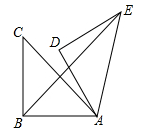
三、计算题
-
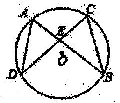
19. 解方程：x2-4x=020. 如图，在⊙O中，弦AB与DC相交于E，且BE=DE，求证：
21. 如图，在平面直角坐标系中，Rt△ABC三个顶点都在格点上，点A、B、C的坐标分别为A(-4，1)，B(-1，1)，C(-1，3)请解答下列问题：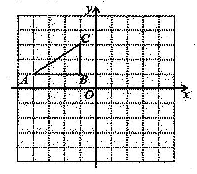
①画出△ABC关于原点0的中心对称图形△A1B1C1并写出点C的对应点C1的坐标；
②画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2 ， 并直接写出点A2的坐标。
22. 某中学为了解本校学生阅读教育、科技、体育、艺术四类课外书的喜爱情况，随机抽取了部分学生进行问卷调查，在此次调查中，甲、乙两班分别有2人特别喜爱阅读科技书报，若从这4人中随机抽取2人去参加科普比赛活动，请用列表法或画树状图的方法，求所抽取的2人来自不同班级的概率。23. 电动车已成为市民日常出行的首选工具，据某市宝骏电动车e100经销商统计，该品牌电动车1月份销售了150辆，3月份销售了216辆。(1)、求该品牌电动车月销售量的平均增长率。(2)、若该品牌电动车的进价为4.3万元，售价为5.8万元，则该经销商1月至3月共盈利多少万元?
24. 某商品的进货价为每件30元，为了合理定价，先投放市场试销．据市场调查，销售价为每件40元时，每周的销售量是l80件，而销售价每上涨l元，则每周的销售量就会减少5件，设每件商品的销售价上涨x元，每周的销售利润为y元。(1)、求y关于X的函数关系式；(2)、应怎样确定销售价，使该商品的每周销售利润最大?最大利润是多少?
