广西河池市凤山县2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、选择题
-
1. 如果+20%表示增加20%,那么-6%表示( )A、增加14% B、增加6% C、减少6% D、减少26%2. 经过同一平面内任意三点中的两点共可以画( )条直线。A、一 B、两 C、三 D、一或三3. 在|-2|,-|0|,(-2)5 , -|-2|,-(-2)这5个数中负数共有( )A、1个 B、2个 C、3个 D、4个4. 方程2x+a-4=0的解是x=-2,则a等于( )A、-8 B、0 C、 2 D、 85. 若|x|=-x,则x的取值范围是( )A、x>0 B、x<0 C、x≥0 D、x≤06. 已知关于x的方程(k-2)x|k|-1+5=3k是一元一次方程,则k等于( )A、±2 B、1 C、-2 D、27. 若 xm+1yn+2和xy3是同类项,则m+n=( ).A、0 B、1 C、
 D、2
8. 一个正方体六个面上分别写着1,2,3,4,5,6,从三个不同角度看正方体如图所示,请判断:1对面的数字是( )
D、2
8. 一个正方体六个面上分别写着1,2,3,4,5,6,从三个不同角度看正方体如图所示,请判断:1对面的数字是( )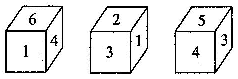 A、2 B、3 C、4 D、59. 如果代数式8y2-4y+5的值是13,那么代数式2y2-y+1的值等于( )A、2 B、3 C、-2 D、410. 如果∠1与∠2互余,∠2与∠3互余,那么∠1,∠3的关系是( )A、互余 B、互补 C、相等 D、无法确定11. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和8港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )A、
A、2 B、3 C、4 D、59. 如果代数式8y2-4y+5的值是13,那么代数式2y2-y+1的值等于( )A、2 B、3 C、-2 D、410. 如果∠1与∠2互余,∠2与∠3互余,那么∠1,∠3的关系是( )A、互余 B、互补 C、相等 D、无法确定11. 轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和8港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )A、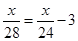 B、
B、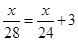 C、
C、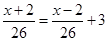 D、
D、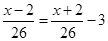 12. 如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为( )
12. 如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为( )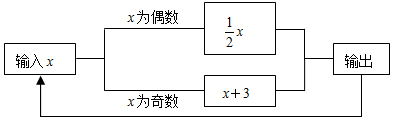 A、6 B、4 C、3 D、1
A、6 B、4 C、3 D、1二、填空题
-
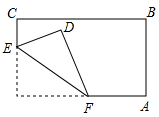
13. -2018的倒数是14. 已知两根木条分别长60cm,100cm,将它们的一端重合,放在同一条直线上,此时两根木条的中点间的距离是 .15. 已知数轴上有一点A,点A到原点的距离为3个单位长度,那么点A表示的数是 .16. 拿一张长方形纸片,按图中所示的方法折叠一角,得到折痕EF, 如果∠DFE=35°,则∠DFA= .
 17. 已知一条射线OA,在同一平面内从点O再作两条射线OB和OC,使∠AOB=80°,∠BOC=30°,则∠AOC的度数是 .18. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
17. 已知一条射线OA,在同一平面内从点O再作两条射线OB和OC,使∠AOB=80°,∠BOC=30°,则∠AOC的度数是 .18. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为 .
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为 . 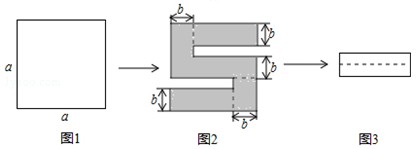
三、解答题
-
19. 计算(1)、-12-(1-0.5)× ×[3-(-3)2](2)、(-2ab+3a)-2(2a-b)+2ab20. 解方程(1)、4x-3(20-x)+4=0(2)、21. 若|x-4|+(2y-x)2=0,求代数式x2-2xy+y2的值22. 先化简,再求值:5(3x2y-xy2)-(xy2+3x2y);其中x= ,y=-l23. 阅读:在用尺规作线段AB等于线段a时,小明的具体做法如下:
已知:如图,线段a:
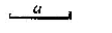
求作:线段AB,使得线段AB=a.
作法:①作射线AM;
②在射线AM上截取AB=a.
∴线段AB即为所求,如右图.
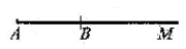
解决下列问题:
已知:如图,线段b:
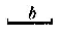
请你仿照小明的作法,在上图中的射线AM上求作点D,使得BD=b;(不要求写作法和结论,保留作图痕迹)
24. 已知:如图,AB⊥CD于点O,∠1=∠2,OE平分∠BOF,∠EOB=55°,求∠DOG的度数.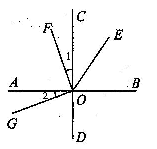 25. 在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?26. 如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边0M与OC都在直线AB的上方.
25. 在手工制作课上,老师组织七年级(2)班的学生用硬纸制作圆柱形茶叶筒.七年级(2)班共有学生44人,其中男生人数比女生人数少2人,并且每名学生每小时剪筒身50个或剪筒底120个.要求一个筒身配两个筒底,为了使每小时剪出的筒身与筒底刚好配套,应该分配多少名学生剪筒身,多少名学生剪筒底?26. 如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角板(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边0M与OC都在直线AB的上方.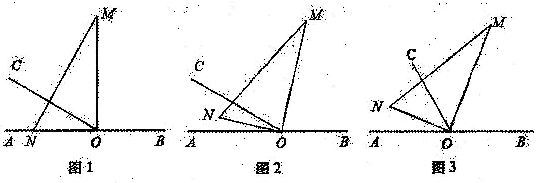 (1)、将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时0N是否平分∠AOC?请说明理由;(2)、在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;(3)、在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由.
(1)、将图1中的三角板绕点O以每秒3°的速度沿顺时针方向旋转一周.如图2,经过t秒后,OM恰好平分∠BOC.①求t的值;②此时0N是否平分∠AOC?请说明理由;(2)、在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒6°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠MON?请说明理由;(3)、在(2)问的基础上,经过多长时间OC平分∠MOB?请画图并说明理由.