浙江省温州市鹿城区2018届数学中考模拟试卷(5)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 如果|a|≥0,那么( )A、a>0 B、a<0 C、a≠0 D、a为任意数2.
如图放置的几何体的左视图是( )
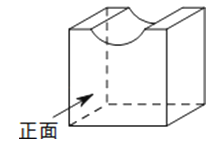 A、
A、 B、
B、 C、
C、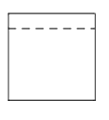 D、
D、 3. 下列事件中,属于必然事件的是( )A、明天太阳从北边升起 B、实心铅球投入水中会下沉 C、篮球队员在罚球线投篮一次,投中 D、抛出一枚硬币,落地后正面向上4. 不等式3x﹣1≥x+3的解集是( )A、x≤4 B、x≥4 C、x≤2 D、x≥25. 某校对八年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):4、4、3.5、5、5、4,这组数据的众数是( )A、4 B、3.5 C、5 D、36. 一次函数y=﹣2x+5的图象与y轴的交点坐标是( )A、(5,0) B、(0,5) C、 ( ,0) D、 (0, )7. 方程组 的解中x与y的值相等,则k等于( )A、2 B、1 C、3 D、48. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”.如图是一个七巧板迷宫,它恰好拼成了一个正方形ABCD,其中点E,P分别是AD,CD的中点,AB=2 ,一只蚂蚁从A处沿图中实线爬行到出口P处,则它爬行的最短路径长为( )
3. 下列事件中,属于必然事件的是( )A、明天太阳从北边升起 B、实心铅球投入水中会下沉 C、篮球队员在罚球线投篮一次,投中 D、抛出一枚硬币,落地后正面向上4. 不等式3x﹣1≥x+3的解集是( )A、x≤4 B、x≥4 C、x≤2 D、x≥25. 某校对八年级6个班学生平均一周的课外阅读时间进行了统计,分别为(单位:h):4、4、3.5、5、5、4,这组数据的众数是( )A、4 B、3.5 C、5 D、36. 一次函数y=﹣2x+5的图象与y轴的交点坐标是( )A、(5,0) B、(0,5) C、 ( ,0) D、 (0, )7. 方程组 的解中x与y的值相等,则k等于( )A、2 B、1 C、3 D、48. 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”.如图是一个七巧板迷宫,它恰好拼成了一个正方形ABCD,其中点E,P分别是AD,CD的中点,AB=2 ,一只蚂蚁从A处沿图中实线爬行到出口P处,则它爬行的最短路径长为( )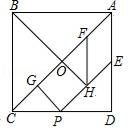 A、3 B、2+
A、3 B、2+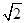 C、4
D、3
C、4
D、3 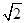 9. 如图,在平行四边形ABCD中,BD=6,将平行四边形ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
9. 如图,在平行四边形ABCD中,BD=6,将平行四边形ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( ) A、3π B、3 C、6π D、610. 如图,A为某旅游景区的最佳观景点,游客可以在B处乘坐缆车沿BD方向先到达小观景平台DE观景,然后再由E处继续乘坐缆车沿EA方向到达A处,返程时从A处乘坐升降电梯直接到C处.已知AC⊥BC于C,DE∥BC,斜坡BD的坡度i=4:3,BC=210米,DE=48米,BD=100米,α=64°,则AC的高度为( )米(结果精确到0.1米,参考数据:sin64°≈0.9,tan64°≈2.1)
A、3π B、3 C、6π D、610. 如图,A为某旅游景区的最佳观景点,游客可以在B处乘坐缆车沿BD方向先到达小观景平台DE观景,然后再由E处继续乘坐缆车沿EA方向到达A处,返程时从A处乘坐升降电梯直接到C处.已知AC⊥BC于C,DE∥BC,斜坡BD的坡度i=4:3,BC=210米,DE=48米,BD=100米,α=64°,则AC的高度为( )米(结果精确到0.1米,参考数据:sin64°≈0.9,tan64°≈2.1)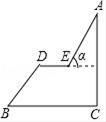 A、214.2 B、235.2 C、294.2 D、315.2
A、214.2 B、235.2 C、294.2 D、315.2二、填空题
-
11. 化简:a+1+a(a+1)+a(a+1)2+…+a(a+1)99= .12. 在对某年级500名学生关于某一现象调查结果的扇形统计图中,有一部分所在扇形圆心角的度数为108°,则这部分学生有人.13. 如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连结AF,则∠DFA= .
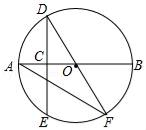 14. 已知某轮船顺水航行a千米,所需的时间和逆水航行b千米所需的时间相同.若水流的速度为c千米/时,则船在静水中的速度为千米/时.15. 一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(﹣1,m),B(n,﹣1)两点,则使kx+b> 的x的取值范围是 .16. 如图,四边形ABCD、CDEF、EFGH都是正方形,则tan∠CAF= .
14. 已知某轮船顺水航行a千米,所需的时间和逆水航行b千米所需的时间相同.若水流的速度为c千米/时,则船在静水中的速度为千米/时.15. 一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(﹣1,m),B(n,﹣1)两点,则使kx+b> 的x的取值范围是 .16. 如图,四边形ABCD、CDEF、EFGH都是正方形,则tan∠CAF= .
三、解答题
-
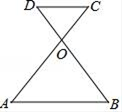
17. 计算:(1)、 +(﹣3)2﹣( ﹣1)0(2)、化简:(2+m)(2﹣m)+m(m﹣1).18. 如图,已知AC和BD相交于点O,且AB∥DC,OA=OB.
求证:OC=OD.
 19. 某校初一年级随机抽取30名学生,对5种活动形式:A、跑步,B、篮球,C、跳绳,D、乒乓球,E、武术,进行了随机抽样调查,每个学生只能选择一种运动行驶,调查统计结果,绘制了不完整的统计图.
19. 某校初一年级随机抽取30名学生,对5种活动形式:A、跑步,B、篮球,C、跳绳,D、乒乓球,E、武术,进行了随机抽样调查,每个学生只能选择一种运动行驶,调查统计结果,绘制了不完整的统计图.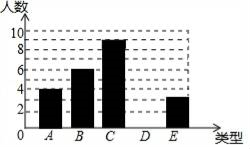 (1)、将条形图补充完整;(2)、如果初一年级有900名学生,估计喜爱跳绳运动的有多少人?(3)、某次体育课上,老师在5个一样的乒乓球上分别写上A、B、C、D、E,放在不透明的口袋中,每人每次摸出一个球并且只摸一次,然后放回,按照球上的标号参加对应活动,小明和小刚是好朋友,请用树状图或列表法的方法,求他俩恰好是同一种活动形式的概率.20. 如图
(1)、将条形图补充完整;(2)、如果初一年级有900名学生,估计喜爱跳绳运动的有多少人?(3)、某次体育课上,老师在5个一样的乒乓球上分别写上A、B、C、D、E,放在不透明的口袋中,每人每次摸出一个球并且只摸一次,然后放回,按照球上的标号参加对应活动,小明和小刚是好朋友,请用树状图或列表法的方法,求他俩恰好是同一种活动形式的概率.20. 如图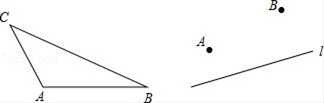 (1)、如图,已知△ABC,请你作出AB边上的高CD,AC边上的中线BE,角平分线AF(不写作法,保留痕迹)(2)、如图,直线l表示一条公路,点A,点B表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A,B的距离之和最短,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)21. 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)、如图,已知△ABC,请你作出AB边上的高CD,AC边上的中线BE,角平分线AF(不写作法,保留痕迹)(2)、如图,直线l表示一条公路,点A,点B表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A,B的距离之和最短,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)21. 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。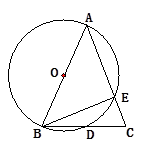 (1)、求∠EBC的度数;(2)、求证:BD=CD。22. 抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B( ,0),且与y轴相交于点C.
(1)、求∠EBC的度数;(2)、求证:BD=CD。22. 抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B( ,0),且与y轴相交于点C.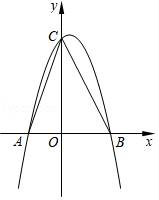 (1)、求这条抛物线的表达式;(2)、求∠ACB的度数;(3)、设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.23. 在平面直角坐标系xOy中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙ O′交x轴于D点,过点D作DF⊥AE于F.
(1)、求这条抛物线的表达式;(2)、求∠ACB的度数;(3)、设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.23. 在平面直角坐标系xOy中,矩形ABCO的面积为15,边OA比OC大2,E为BC的中点,以OE为直径的⊙ O′交x轴于D点,过点D作DF⊥AE于F.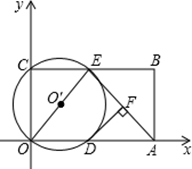 (1)、求OA,OC的长;(2)、求证:DF为⊙ O′的切线;(3)、小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.
(1)、求OA,OC的长;(2)、求证:DF为⊙ O′的切线;(3)、小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.