浙江省宁波市余姚市2018届数学中考模拟试卷(6月份)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 在3.14, ,﹣ ,π这四个数中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 函数y=中自变量x的取值范围是( )A、x≥2 B、x≥﹣2 C、x<2 D、x<﹣23. 下列运算结果正确的是( )A、a3+a4=a7 B、a4÷a3=a C、a3•a2=2a3 D、(a3)3=a64. PM2.5是指大气中直径小于或等于2.5μm(1μm=0.000001m)的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质,对人体健康和大气环境质量有很大危害.2.5μm用科学记数法可表示为( )A、2.5×10﹣5m B、0.25×10﹣7m C、2.5×10﹣6m D、25×10﹣5m5. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
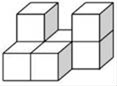 A、主视图 B、俯视图 C、左视图 D、一样大6. 某青年排球队12名队员的年龄情况如表:
A、主视图 B、俯视图 C、左视图 D、一样大6. 某青年排球队12名队员的年龄情况如表:年龄
18
19
20
21
22
人数
1
4
3
2
2
则这个队队员年龄的众数和中位数是( )
A、19,20 B、19,19 C、19,20.5 D、20,197. 如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( ) A、α+β=180° B、α+β=90° C、β=3α D、α﹣β=90°8. 已知两个相似三角形的周长比为2:3,它们的面积之差为40cm2 , 那么它们的面积之和为( )A、108cm2 B、104cm2 C、100cm2 D、80cm29. 如图,在▱ABCD中,M是BC延长线上的一点,若∠A=125°,则∠MCD的度数是( )
A、α+β=180° B、α+β=90° C、β=3α D、α﹣β=90°8. 已知两个相似三角形的周长比为2:3,它们的面积之差为40cm2 , 那么它们的面积之和为( )A、108cm2 B、104cm2 C、100cm2 D、80cm29. 如图,在▱ABCD中,M是BC延长线上的一点,若∠A=125°,则∠MCD的度数是( )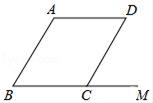 A、45° B、65° C、55° D、75°10. 二次函数y=﹣x2+(12﹣m)x+12,时,当x>2时,y随x的增大而减小;当x<2时,y随x的增大而增大,则m的值为( )A、6 B、8 C、10 D、1211. 如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )
A、45° B、65° C、55° D、75°10. 二次函数y=﹣x2+(12﹣m)x+12,时,当x>2时,y随x的增大而减小;当x<2时,y随x的增大而增大,则m的值为( )A、6 B、8 C、10 D、1211. 如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )
a篮球运动员投篮时,投出去的篮球的高度与时间的关系
b去超市购买同一单价的水果,所付费用与水果数量的关系
c李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系
d周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A、abcd B、acdb C、acbd D、adbc12. 如图,在矩形ABCD中,E,F分别是AD,BC的中点,AF与BE相交于点M,CE与DF相交于点N,QM⊥BE,QN⊥EC相交于点Q,PM⊥AF,PN⊥DF相交于点P,若2BC=3AB,记△ABM和△CDN的面积和为S,则四边形MQNP的面积为( )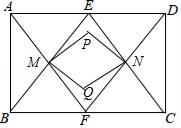 A、 S B、
A、 S B、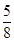 S
C、
S
C、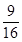 S
D、 S
13. 关于x,y的方程组 的解满足x+y=6,则 m的值为( )A、﹣1 B、2 C、1 D、4
S
D、 S
13. 关于x,y的方程组 的解满足x+y=6,则 m的值为( )A、﹣1 B、2 C、1 D、4二、填空题
-
14. |x+1|+|x﹣2|+|x﹣3|的值为 .15. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有个.16. 已知圆锥的侧面积是40π,底面圆直径为2,则圆锥的母线长是 .17. 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合, 点A在x轴上,点B在反比例函数 位于第一象限的图象上,则正六边形ABCDEF的边长为;
 18. 如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE= .
18. 如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE= .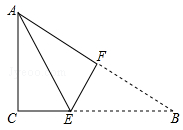
三、解答题
-
19. 为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
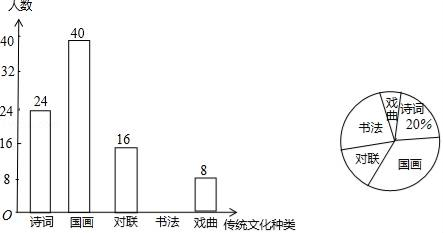 (1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?20. 对x,y定义一种新运算F,规定:F(x,y)=(mx+ny)(3x﹣y)(其中m,n均为非零常数).例如:F(1,1)=2m+2n,F(﹣1,0)=3m.(1)、已知F(1,﹣1)=﹣8,F(1,2)=13.
(1)、本次调查共抽取了多少名学生?(2)、通过计算补全条形统计图;(3)、若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?20. 对x,y定义一种新运算F,规定:F(x,y)=(mx+ny)(3x﹣y)(其中m,n均为非零常数).例如:F(1,1)=2m+2n,F(﹣1,0)=3m.(1)、已知F(1,﹣1)=﹣8,F(1,2)=13.①求m,n的值;
②关于a的不等式组 ,求a的取值范围;
(2)、当x2≠y2时,F(x,y)=F(y,x)对任意有理数x,y都成立,请直接写出m,n满足的关系式.21. 如图,在由边长为1个单位长度的小正方形组成的12×2网格中,给出了格点△ABC和直线l.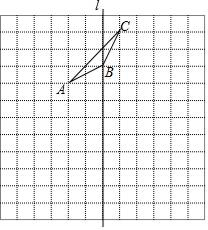
①画出△ABC关于直线l对称的格点△A′B′C;
②在直线l上选取一格点,在网格内画出格点△DPE,使得△DPE∽△ABC,且相似比为2:1.
22. 如图,AC=BC,D是AB中点,CE∥AB,CE= AB.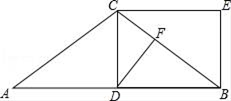 (1)、求证:四边形CDBE是矩形.(2)、若AC=5,CD=3,F是BC上一点,且DF⊥BC,求DF的长.23. 夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:
(1)、求证:四边形CDBE是矩形.(2)、若AC=5,CD=3,F是BC上一点,且DF⊥BC,求DF的长.23. 夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:项目品种
单价(元/棵)
成活率
A
m
91%
B
100
97%
(1)、求表中m的值;(2)、预计对这段公路的绿化需购1000棵这样的风景树.若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?最低费用为多少?