浙江省宁波市余姚市2018届数学中考模拟试卷（4月份）

试卷更新日期：2019-03-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列实数中，无理数是（）

A、2 B、 C、3.14 D、

查看试题解析
2. 函数 $y = \sqrt{x - 2}$ 中，自变量x的取值范围是（）

A、x≥2 B、x＞2 C、x＜2 D、x≠2

查看试题解析
3. 下列运算正确的是（）

A、a²+a³=a⁵ B、a²•a³=a⁶ C、a⁴÷a²=a² D、（a²）⁴=a⁶

查看试题解析
4. 2018年1月份，宁波部分中小学爆发大规模流感疫情，流感病毒的形状一般为球形，直径大约为0.000000102米，该直径用科学记数法表示为（）米

A、 1.02×10^﹣⁷ B、1.02×10⁷ C、1.02×10^﹣⁸ D、1.02×10⁸

查看试题解析
5. 如图所示，该几何体的俯视图是（）

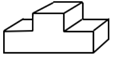A、 B、 C、 D、

查看试题解析
6. 在学校开展的“争做最优秀中学生”的一次演讲比赛中，编号分别为1，2，3，4，5的五位同学最后成绩如下表所示：

参赛者编号

1

2

3

4

5

成绩（分）

96

88

86

93

86

那么这五位同学演讲成绩的众数与中位数依次是（）

A、96，88 B、92，88 C、88，86 D、86，88

查看试题解析
7. 如图，已知直线a∥b，直角三角形顶点C在直线b上，且∠A=60°，若∠1=57°，则∠2的度数是（）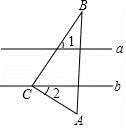

A、30° B、33° C、37° D、43°

查看试题解析
8. 若两个相似三角形对应边上的高线之比为3：1，则对应角的平分线之比为（）

A、9：1 B、6：1 C、3：1 D、：1

查看试题解析
9. 如图，在▱ABCD中，点E是DC边上一点，连接AE，BE，若AE，BE分别是∠DAB，∠CBA的角平分线，且AB=4，则▱ABCD的周长为（）

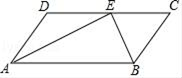A、10 B、 8 C、 5 D、12

查看试题解析
10. 平面直角坐标系中，二次函数y=ax²+4ax+4a﹣4的图象经过四个象限，则a的取值范围为（）

A、a＜1 B、0＜a＜1 C、a≥1 D、﹣1＜a＜0

查看试题解析
11. 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数（单位：km/L），如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况，下列叙述正确的是（）

A、以相同速度行驶相同路程，甲车消耗汽油最多 B、以10km/h的速度行驶时，消耗1升汽油，甲车最少行驶5千米 C、以低于80km/h的速度行驶时，行驶相同路程，丙车消耗汽油最少 D、以高于80km/h的速度行驶时，行驶相同路程，丙车比乙车省油

查看试题解析
12. 如图所示，矩形ABCD被分割成五个矩形，且MH=PF，则下列等式中：① $\frac{M N}{A E} = \frac{N P}{B F}$ ② $\frac{E N}{N P} = \frac{P F}{P Q}$ 可以判断甲、乙两个矩形面积相等的是（）

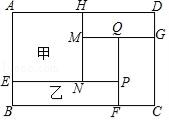A、①②都不可以 B、仅①可以 C、仅②可以 D、①②都可以

查看试题解析

二、填空题

13. －3的绝对值是．

查看试题解析
14. 不透明的布袋中有2个红球和3个白球，所有球除颜色外无其它差别．某同学从布袋里任意摸出一个球，则他摸出红球的概率是．

查看试题解析
15. 如果实数x，y满足方程组 ${\begin{matrix} 2 x + y = 4 \\ 2 y + x = 5 \end{matrix}$ ，那么x﹣y的值为．

查看试题解析
16. 若圆锥底面圆的直径和母线长均为4cm，则它的侧面展开图的面积等于 cm² ．

查看试题解析
17. 如图，正六边形OABCDE中，点E（﹣2，0），将该正六边形向右平移a（a＞0）个单位后，恰有两个顶点落在反比例函数y= $\frac{k}{x}$ （k＞0）的图象上，则k的值为．

查看试题解析
18. 如图，将△ABC沿着CE翻折，使点A落在点D处，CD与AB交于点F，恰好有CE=CF，若DF=6，AF=14，则tan∠CEF= ．

查看试题解析

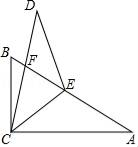
三、解答题

19. 先化简，再求值：（1+ $\frac{1}{x - 1}$ ）÷ $\frac{2 x}{x^{2} - 1}$ ，其中x= $\sqrt{2}$ ﹣1．

查看试题解析
20. 为了解余姚市对“垃圾分类知识”的知晓程度，某数学学习兴趣小组对市民进行随机抽样的问卷调查，调查结果分为“A．非常了解”、“B．了解”、“C．基本了解”、“D．不太了解”四个等级进行统计，并将统计结果绘制成了如下两幅不完整的统计图（图1、图2），请根据图中的信息解答下列问题．

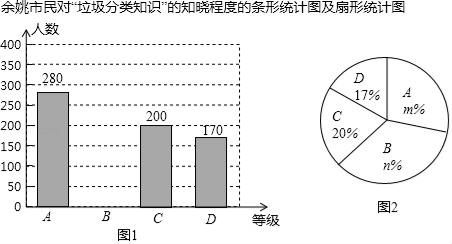(1)、这次调查的市民人数为人，图2中，m=

(2)、补全图1中的条形统计图；

(3)、据统计，2017年余姚约有市民140万人，那么根据抽样调查的结果，可估计对“垃圾分类知识”的知晓程度为“B．了解”的市民约有多少万人？

查看试题解析
21. 请你阅读如图框内老师的新定义运算规定，然后解答下列各小题．

(1)、若x⊕y=1，x⊕2y=﹣2，分别求出x和y的值；

(2)、若x满足x⊕2≤0，且3x⊕（﹣8）＞0，求x的取值范围．

查看试题解析
22. 在4×4的方格中，△ABC的三个顶点都在格点上．

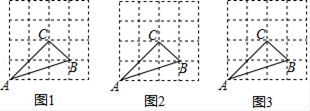
①在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形（画出一个即可）；

②在图2、图3中各作一格点D，使得△ACD∽△DCB，并请连结AD、CD、BD．

查看试题解析
23. 如图，在△ABC中，AB=AC，AD是BC边的中线，过点A作BC的平行线，过点B作AD的平行线，两线交于点E．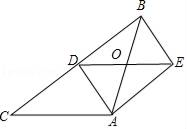

(1)、求证：四边形ADBE是矩形；

(2)、连结DE，交AB与点O，若BC=8，AO= $\frac{5}{2}$ ，求△ABC的面积．

查看试题解析
24. 某商城销售A，B两种自行车，A型自行车售价为2200元/辆，B型自行车售价为1750元/辆，每辆A型自行车的进价比每辆B型自行车的进价多400元，商城用80000元购进A型自行车的数量与用64000元购进B型自行车的数量相等．

(1)、求A，B两种自行车的进价分别是多少元/辆？

(2)、现在商城准备一次购进这两种自行车共100辆，设购进A型自行车m辆，这100辆自行车的销售总利润为w元，要求购进B型自行车数量不少于A型自行车数量的2倍，且A型车辆至少30辆，请用含m的代数式表示w，并求获利最大的方案以及最大利润．

查看试题解析
25. 如图，抛物线y=ax²﹣2ax+3的图象与x轴分别交于点A，B，与y轴交于点C，已知BO=CO．

(1)、求抛物线的解析式；

(2)、点E在线段OB上，过点E作x轴的垂线交抛物线于点P，连结PA，若PA⊥CE，垂足为点F，求OE的长．

查看试题解析
26. 定义：有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形．

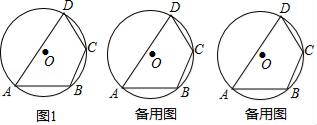(1)、如图1，四边形ABCD内接于⊙O，∠DCB﹣∠ADC=∠A，求证：四边形ABCD为圆内接倍角四边形；

(2)、在（1）的条件下，⊙O半径为5．
①若AD为直径，且sinA= $\frac{4}{5}$ ，求BC的长；

(3)、在（1）的条件下，记AB=a，BC=b，CD=c，AD=d，求证：d²﹣b²=ab+cd．

查看试题解析

参赛者编号	1	2	3	4	5
成绩（分）	96	88	86	93	86