浙江省宁波市南三县2018届数学中考模拟试卷(4)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 计算:﹣15÷(﹣5)结果正确的是( )A、75 B、﹣75 C、3 D、﹣32. 下列交通标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
3. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )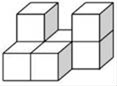 A、主视图 B、俯视图 C、左视图 D、一样大4. 下列运算中正确的是( )A、a5+a5=2a10 B、a5•a5=2a10 C、(﹣4a﹣1)(4a﹣1)=1﹣16a2 D、(a﹣2b)2=a2﹣4b25. 如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
A、主视图 B、俯视图 C、左视图 D、一样大4. 下列运算中正确的是( )A、a5+a5=2a10 B、a5•a5=2a10 C、(﹣4a﹣1)(4a﹣1)=1﹣16a2 D、(a﹣2b)2=a2﹣4b25. 如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )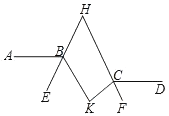 A、76° B、78° C、80° D、82°6. 抛物线y=x2+4x+5是由抛物线y=x2+1经过某种平移得到,则这个平移可以表述为( )A、向左平移1个单位 B、向左平移2个单位 C、向右平移1个单位 D、向右平移2个单位7. 下列命题中,真命题的个数有( )
A、76° B、78° C、80° D、82°6. 抛物线y=x2+4x+5是由抛物线y=x2+1经过某种平移得到,则这个平移可以表述为( )A、向左平移1个单位 B、向左平移2个单位 C、向右平移1个单位 D、向右平移2个单位7. 下列命题中,真命题的个数有( )①如果两条直线都与第三条直线平行,那么这两条直线也互相平行.②过直线外一点有且只有一条直线与这条直线平行.③两条直线被第三条直线所截,同旁内角互补.④内错角相等,两直线平行.
A、4 B、3 C、2 D、18. 如图:二次函数y=ax2+bx+2的图象与x轴交于A、B两点,与y轴交于C点,若AC⊥BC,则a的值为( )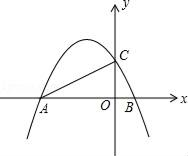 A、﹣ B、﹣ C、﹣1 D、﹣29. 如图,AB为⊙O的直径,过B作⊙O的切线,在该切线上取点C,连接AC交⊙O于D,若⊙O的半径是6,∠C=36°,则劣弧AD的长是( )
A、﹣ B、﹣ C、﹣1 D、﹣29. 如图,AB为⊙O的直径,过B作⊙O的切线,在该切线上取点C,连接AC交⊙O于D,若⊙O的半径是6,∠C=36°,则劣弧AD的长是( )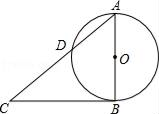 A、
A、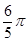 B、
B、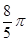 C、
C、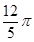 D、3π
D、3π
二、填空题
-
10. 据最新统计,苏州市常住人口约为1062万人.数据10 620 000用科学记数法可表示为 .11. 教室里有几名学生,这个时候一位身高170厘米的老师走进了教室,使得教室里所有人的平均身高从140厘米变成了145厘米,使得所有人的平均体重从35千克变成了39千克,则老师的体重是千克.12. 如图,在Rt△ABC中,∠ACB=90°,半径为1的圆A与边AB相交于点D,与边AC相交于点E,连接DE并延长,与线段BC的延长线交于点P.已知tan∠BPD= ,CE=2,则△ABC的周长是
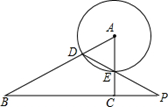 13. 如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是 .
13. 如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长是 . 14. 已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y= 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为 .
14. 已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y= 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为 .
三、解答题
-
15. 化简计算
①π0+2﹣1﹣ ﹣|1﹣ |
② ﹣2
③ ﹣ ( +2)
④3 ﹣9 +3
⑤ ÷ ﹣ × + .
16. 解不等式组 ;17. 已知:如图,在▱ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.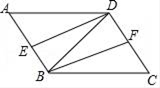 (1)、求证:△ADE≌△CBF;(2)、当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.18. 如图,反比例函数y= (k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)
(1)、求证:△ADE≌△CBF;(2)、当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.18. 如图,反比例函数y= (k≠0)的图象过等边三角形AOB的顶点A,已知点B(﹣2,0)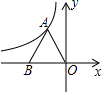 (1)、求反比例函数的表达式;(2)、若要使点B在上述反比例函数的图象上,需将△ABC向上平移多少个单位长度?19. 某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
(1)、求反比例函数的表达式;(2)、若要使点B在上述反比例函数的图象上,需将△ABC向上平移多少个单位长度?19. 某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.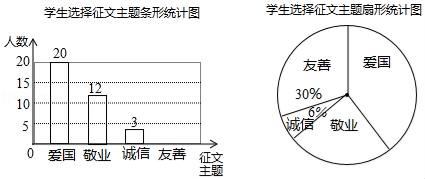 (1)、求共抽取了多少名学生的征文;(2)、将上面的条形统计图补充完整;(3)、在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;(4)、如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.20. 如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.
(1)、求共抽取了多少名学生的征文;(2)、将上面的条形统计图补充完整;(3)、在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;(4)、如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.20. 如图,已知A、B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于D.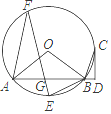 (1)、求证:CD是⊙O的切线;(2)、E为 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= ,BE=BG,EG=3 ,求⊙O的半径.
(1)、求证:CD是⊙O的切线;(2)、E为 的中点,F为⊙O上一点,EF交AB于G,若tan∠AFE= ,BE=BG,EG=3 ,求⊙O的半径.
21. A、B两辆汽车同时从相距330千米的甲、乙两地相向而行,s(千米)表示汽车与甲地的距离,t(分)表示汽车行驶的时间,如图,L1 , L2分别表示两辆汽车的s与t的关系.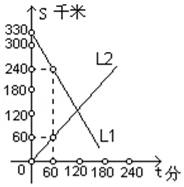 (1)、L1表示哪辆汽车到甲地的距离与行驶时间的关系?(2)、汽车B的速度是多少?(3)、求L1 , L2分别表示的两辆汽车的s与t的关系式.(4)、2小时后,两车相距多少千米?(5)、行驶多长时间后,A、B两车相遇?22. 抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B( ,0),且与y轴相交于点C.
(1)、L1表示哪辆汽车到甲地的距离与行驶时间的关系?(2)、汽车B的速度是多少?(3)、求L1 , L2分别表示的两辆汽车的s与t的关系式.(4)、2小时后,两车相距多少千米?(5)、行驶多长时间后,A、B两车相遇?22. 抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B( ,0),且与y轴相交于点C.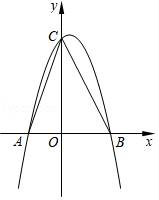 (1)、求这条抛物线的表达式;(2)、求∠ACB的度数;(3)、设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.
(1)、求这条抛物线的表达式;(2)、求∠ACB的度数;(3)、设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.