浙江省杭州市萧山区2018届数学中考模拟试卷(6月份)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 相反数不大于它本身的数是( )A、 正
 数
B、负数
C、非正数
D、非负数
2. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是( )
数
B、负数
C、非正数
D、非负数
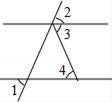
2. 由一些大小相同的小正方体搭成的几何体的主视图和左视图如图,则搭成该几何体的小正方体的个数最少是( )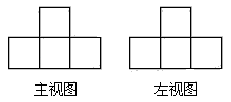 A、3 B、4 C、5 D、63. 下列计算中,不正确的是( )A、a2•a5=a10 B、a2﹣2ab+b2=(a﹣b)2 C、﹣(a﹣b)=﹣a+b D、﹣3a+2a=﹣a4. 如图直线AB,CD,EF被直线a、b所截,若∠1=100°,∠2=100°,∠3=125°,∠4=55°,下列结论错误的是( )
A、3 B、4 C、5 D、63. 下列计算中,不正确的是( )A、a2•a5=a10 B、a2﹣2ab+b2=(a﹣b)2 C、﹣(a﹣b)=﹣a+b D、﹣3a+2a=﹣a4. 如图直线AB,CD,EF被直线a、b所截,若∠1=100°,∠2=100°,∠3=125°,∠4=55°,下列结论错误的是( )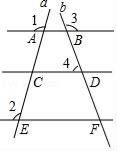 A、EF∥CD∥AB B、
A、EF∥CD∥AB B、 C、
C、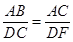 D、
D、 5. 下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是( )
5. 下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是( )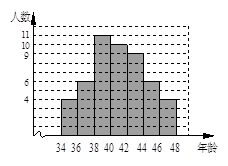 A、该学校教职工总人数是50人 B、年龄在40≤x<42小组的教职工人数占该学校总人数的20% C、教职工年龄的中位数一定落在40≤x<42这一组 D、教职工年龄的众数一定在38≤x<40这一组6. 点P的坐标为(﹣3,2),把点P向右平移2个单位后再向下平移5个单位得到点P1 , 则点P1的坐标为( )A、(﹣1,2) B、(﹣5,﹣3) C、(﹣1,﹣3) D、(﹣1,7)7. 如图,在Rt△ABC中,∠C=90°,点B在CD上,且BD=BA=2AC,则tan∠DAC的值为( )
A、该学校教职工总人数是50人 B、年龄在40≤x<42小组的教职工人数占该学校总人数的20% C、教职工年龄的中位数一定落在40≤x<42这一组 D、教职工年龄的众数一定在38≤x<40这一组6. 点P的坐标为(﹣3,2),把点P向右平移2个单位后再向下平移5个单位得到点P1 , 则点P1的坐标为( )A、(﹣1,2) B、(﹣5,﹣3) C、(﹣1,﹣3) D、(﹣1,7)7. 如图,在Rt△ABC中,∠C=90°,点B在CD上,且BD=BA=2AC,则tan∠DAC的值为( )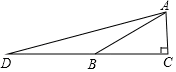 A、2+ B、2 C、3+ D、38. 在矩形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,点P是对角线OC上的任意一点(不包括端点),以P为圆心的圆与AD相切,则⊙P与AB的位置关系是( )A、相离 B、相切 C、相交 D、不确定9. 如图,在等边三角形ABC中,点P是BC边上一动点(不与点B,C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )
A、2+ B、2 C、3+ D、38. 在矩形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,点P是对角线OC上的任意一点(不包括端点),以P为圆心的圆与AD相切,则⊙P与AB的位置关系是( )A、相离 B、相切 C、相交 D、不确定9. 如图,在等边三角形ABC中,点P是BC边上一动点(不与点B,C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )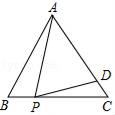 A、
A、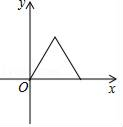 B、
B、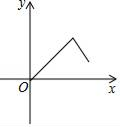 C、
C、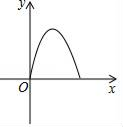 D、
D、 10. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x﹣1)=1035×2 C、x(x﹣1)=1035 D、2x(x+1)=1035
10. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x﹣1)=1035×2 C、x(x﹣1)=1035 D、2x(x+1)=1035二、解答题
-
11. 阅读并完成下列各题:
通过学习,同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷.相信通过下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
(例)用简便方法计算995×1005.
解:995×1005
=(1000﹣5)(1000+5)①
=10002﹣52②
=999975.
(1)、例题求解过程中,第②步变形是利用(填乘法公式的名称);(2)、用简便方法计算:①9×11×101×10 001;
②(2+1)(22+1)(24+1)…(232+1)+1.
12. 某学校为了解该校七年级学生的身高情况,抽样调查了部分同学身高,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1cm):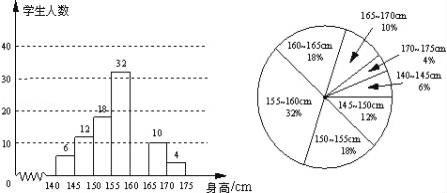 (1)、请根据所提供的信息补全频数分布直方图;(2)、样本的中位数落在(身高值)段中;(3)、如果该校七年级共有500名学生,那么估计全校身高在160cm或160cm以上的七年级学生有人;(4)、如果上述七年级样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么学生的身高比较整齐.(填“七年级”或“八年级”)13. 如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).
(1)、请根据所提供的信息补全频数分布直方图;(2)、样本的中位数落在(身高值)段中;(3)、如果该校七年级共有500名学生,那么估计全校身高在160cm或160cm以上的七年级学生有人;(4)、如果上述七年级样本的平均数为157cm,方差为0.8;该校八年级学生身高的平均数为159cm,方差为0.6,那么学生的身高比较整齐.(填“七年级”或“八年级”)13. 如图,在△ABC中,∠C=90°,AB=10,BC=8,P、Q分别是AB、BC边上的点,且AP=BQ=a (其中0<a<8).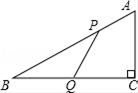 (1)、若PQ⊥BC,求a的值;(2)、若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.14. 解不等式组 ;15. 如图,已知正方形ABCD的边长为 ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)、若PQ⊥BC,求a的值;(2)、若PQ=BQ,把线段CQ绕着点Q旋转180°,试判别点C的对应点C’是否落在线段QB上?请说明理由.14. 解不等式组 ;15. 如图,已知正方形ABCD的边长为 ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,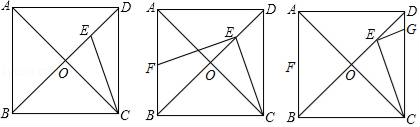 (1)、求DE的长;(2)、过点EF作EF⊥CE,交AB于点F,求BF的长;(3)、过点E作EG⊥CE,交CD于点G,求DG的长.16. 在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).(1)、求抛物线的表达式和顶点坐标;(2)、将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.17. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.
(1)、求DE的长;(2)、过点EF作EF⊥CE,交AB于点F,求BF的长;(3)、过点E作EG⊥CE,交CD于点G,求DG的长.16. 在平面直角坐标系xOy中,抛物线y=ax2+4x+c(a≠0)经过点A(3,﹣4)和B(0,2).(1)、求抛物线的表达式和顶点坐标;(2)、将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿直线x=3翻折,得到图象N.若过点C(9,4)的直线y=kx+b与图象M、图象N都相交,且只有两个交点,求b的取值范围.17. 我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.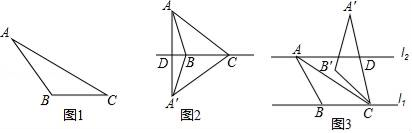 (1)、概念理解:
(1)、概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.
(2)、问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求 的值.
(3)、应用拓展:如图3,已知l1∥l2 , l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的 倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.
三、填空题