浙江省杭州市萧山区2018届数学中考二模试卷
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. -2的相反数是( )A、2 B、-2 C、 D、2. 如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( )
 A、
A、 B、
B、 C、
C、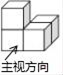 D、
D、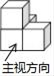 3. 下列变形正确的是( )A、a6=a2•a3 B、1﹣2a+4b=1﹣2(a+2b) C、x2﹣2x﹣3=(x﹣1)2﹣1 D、1﹣a+ a2=( a﹣1)24. 如图,AB与CD相交于点E,AD∥BC, ,CD=16,则DE的长为( )
3. 下列变形正确的是( )A、a6=a2•a3 B、1﹣2a+4b=1﹣2(a+2b) C、x2﹣2x﹣3=(x﹣1)2﹣1 D、1﹣a+ a2=( a﹣1)24. 如图,AB与CD相交于点E,AD∥BC, ,CD=16,则DE的长为( ) A、3 B、6 C、
A、3 B、6 C、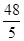 D、10
5. 用一根细铁丝可以折成边长为10cm的等边三角形,也可以折成面积为50cm2的长方形.设所折成的长方形的一边长为xcm,可列方程为( )A、x(10﹣x)=50 B、x(30﹣x)=50 C、x(15﹣x)=50 D、x(30﹣2x)=506. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( )
D、10
5. 用一根细铁丝可以折成边长为10cm的等边三角形,也可以折成面积为50cm2的长方形.设所折成的长方形的一边长为xcm,可列方程为( )A、x(10﹣x)=50 B、x(30﹣x)=50 C、x(15﹣x)=50 D、x(30﹣2x)=506. 如图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/时)情况.则这些车的车速的众数、中位数分别是( ) A、8,6 B、8,5 C、52,53 D、52,527. 在平面直角坐标系中,有一条线段AB,已知点A(﹣3,0)和B(0,4),平移线段AB得到线段A1B1 . 若点A的对应点A1的坐标为(0,﹣1),则线段AB平移经过的区域(四边形ABB1A1)的面积为( )A、12 B、15 C、24 D、308. 如图,四边形ABCD中,∠ABC=90°.已知∠A=α,外角∠DCE=β,BC=a,CD=b,则下列结论错误的是( )
A、8,6 B、8,5 C、52,53 D、52,527. 在平面直角坐标系中,有一条线段AB,已知点A(﹣3,0)和B(0,4),平移线段AB得到线段A1B1 . 若点A的对应点A1的坐标为(0,﹣1),则线段AB平移经过的区域(四边形ABB1A1)的面积为( )A、12 B、15 C、24 D、308. 如图,四边形ABCD中,∠ABC=90°.已知∠A=α,外角∠DCE=β,BC=a,CD=b,则下列结论错误的是( ) A、∠ADC=90°﹣α+β B、点D到BE的距离为b•sinβ C、AD=
A、∠ADC=90°﹣α+β B、点D到BE的距离为b•sinβ C、AD= D、点D到AB的距离为a+bcosβ
9. 如图,△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,点E是线段AD上一点,以点E为圆心,r为半径作⊙E.若⊙E与边AB,AC相切,而与边BC相交,则半径r的取值范围是( )
D、点D到AB的距离为a+bcosβ
9. 如图,△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,点E是线段AD上一点,以点E为圆心,r为半径作⊙E.若⊙E与边AB,AC相切,而与边BC相交,则半径r的取值范围是( ) A、r> B、 <r≤4 C、 <r≤4 D、 <r≤10. 如图1,在矩形ABCD中,动点E从A出发,沿A→B→C方向运动,当点E到达点C时停止运动,过点E作EF⊥AE交CD于点F,设点E运动路程为x,CF=y,如图2所表示的是y与x的函数关系的大致图象,给出下列结论:①a=3;②当CF= 时,点E的运动路程为 或 或 ,则下列判断正确的是( )
A、r> B、 <r≤4 C、 <r≤4 D、 <r≤10. 如图1,在矩形ABCD中,动点E从A出发,沿A→B→C方向运动,当点E到达点C时停止运动,过点E作EF⊥AE交CD于点F,设点E运动路程为x,CF=y,如图2所表示的是y与x的函数关系的大致图象,给出下列结论:①a=3;②当CF= 时,点E的运动路程为 或 或 ,则下列判断正确的是( )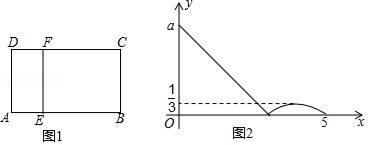 A、①②都对 B、①②都错 C、①对②错 D、①错②对
A、①②都对 B、①②都错 C、①对②错 D、①错②对二、填空题
-
11. 在一个不透明的袋子中装有仅颜色不同的5个小球,其中红球3个,黑球2个,先从袋中取出m(m≥1)个红球,不放回,再从袋子中随机摸出1个球.将“摸出黑球”记为事件A.(1)若A为必然事件,则m的值为;(2)若A发生的概率为 ,则m的值为 .12. 如图,直线a,b分别与直线c,d相交,且∠1+∠3=135°,∠2﹣∠3=45°,若∠3=α,则∠4的度数为 .
 13. 如图,在⊙O的内接六边形ABCDEF中,∠A+∠C=220°,则∠E=°.
13. 如图,在⊙O的内接六边形ABCDEF中,∠A+∠C=220°,则∠E=°. 14. 已知点M是函数y= x与y= 的图象的交点,且OM=4,则点M的坐标为 .15. 在平面直角坐标系xOy中,已知点A(0,﹣2),点B(3m,2m+1),点C(6,2),点D.(1)、线段AC的中点E的坐标为;(2)、▱ABCD的对角线BD长的最小值为 .
14. 已知点M是函数y= x与y= 的图象的交点,且OM=4,则点M的坐标为 .15. 在平面直角坐标系xOy中,已知点A(0,﹣2),点B(3m,2m+1),点C(6,2),点D.(1)、线段AC的中点E的坐标为;(2)、▱ABCD的对角线BD长的最小值为 .三、解答题
-
16. 计算:(﹣2018)2+2017×(﹣2019).17. 某学校为了解本校九年级学生期末考试数学成续情况,决定进行抽样分析,已知该校九年级共有10个班,每班40名学生,请根据要求回答下列问题:(1)、若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有 . (只要填写序号)
①随机抽取一个班级的学生;②在全年级学生中随机抽取40名男学生:③在全年级10个班中各随机抽取4名学生.
(2)、将抽取的40名学生的数学成绩进行分组,并绘制频数表和成分布统计图(不完整)如表格、图:①C、D类圆心角度数分别为;②估计全年级A、B类学生人数大约共有 .成绩(单位:分)
频数
频率
A类(80~100)
0.3
B类(60~79)
0.4
C类(40~59)
8
D类(0~39)
4
(3)、学校为了解其他学校数学成绩情况,将同层次的G学校和J学校的抽样数据进行对比,得下表:你认为哪所学校教学效果较好?说明你的理由.学校
平均数(分)
方差
A、B类频率和
G学校
87
520
0.7
J学校
87
478
0.65
 18. 如图,△ABC中,D是AC上一点,E是BD上一点,∠A=∠CBD=∠DCE.
18. 如图,△ABC中,D是AC上一点,E是BD上一点,∠A=∠CBD=∠DCE. (1)、求证:△ABC∽△CDE;(2)、若BD=3DE,试求 的值.19. 已知关于a的不等式组 .(1)、求此不等式组的解;(2)、试比较a﹣3与 的大小.20. 边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)、求证:△ABC∽△CDE;(2)、若BD=3DE,试求 的值.19. 已知关于a的不等式组 .(1)、求此不等式组的解;(2)、试比较a﹣3与 的大小.20. 边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE. (1)、若点F在边BC上(如图);
(1)、若点F在边BC上(如图);①求证:CE=EF;
②若BC=2BF,求DE的长.
(2)、若点F在CB延长线上,BC=2BF,请直接写出DE的长.21. 在平面直角坐标系中,已知二次函数y=k(x-a)(x-b),其中a≠b.
(1)、若此二次函数图象经过点(0,k),试求a,b满足的关系式.(2)、若此二次函数和函数y=x2﹣2x的图象关于直线x=2对称,求该函数的表达式.(3)、若a+b=4,且当0≤x≤3时,有1≤y≤4,求a的值.22. 如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF. (1)、若∠A=70°,请直接写出∠ABF的度数.(2)、若点F是CD的中点,
(1)、若∠A=70°,请直接写出∠ABF的度数.(2)、若点F是CD的中点,①求sinA的值;
②求证:S△ABE= SABCD .
(3)、设 =k, =m,试用含k的代数式表示m.