浙江省杭州市西湖区2018届数学中考一模试卷
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. ﹣32=( )A、﹣3 B、﹣9 C、3 D、92. 某企业今年1月份产值为x万元,2月份比1月份增加了10%,3月份比2月份减少了20%,则3月份的产值是( )万元.A、(1+10%)(1﹣20%)x B、(1+10%+20%)x C、(x+10%)(x﹣20%) D、(1+10%﹣20%)x3. 如图,已知直线l1 , l2 , l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3 , 若AB=4,AC=6,DF=9,则DE=( )
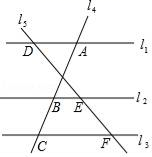 A、5 B、6 C、7 D、84. 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
A、5 B、6 C、7 D、84. 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )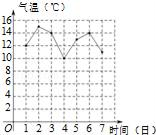 A、13,13 B、14,14 C、13,14 D、14,135. 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
A、13,13 B、14,14 C、13,14 D、14,135. 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )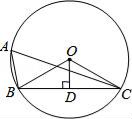 A、2 B、 C、1 D、6. 已知m=|﹣ |÷ ,则( )A、﹣9<m<﹣8 B、﹣8<m<﹣7 C、7<m<8 D、8<m<97. 已知二次函数y=﹣x2+2mx,以下点可能成为函数顶点的是( )A、(﹣2,4) B、(1,2) C、(﹣1,﹣1) D、(2,﹣4)8. 在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则( )A、C与∠α的大小有关 B、当∠α=45°时,S= C、A,B,C,D四个点可以在同一个圆上 D、S随∠α的增大而增大9. 对于二次函数y=x2﹣2mx+3m﹣3,以下说法:①图象过定点( ),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )A、①② B、②③ C、①②④ D、①③④10. 如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )
A、2 B、 C、1 D、6. 已知m=|﹣ |÷ ,则( )A、﹣9<m<﹣8 B、﹣8<m<﹣7 C、7<m<8 D、8<m<97. 已知二次函数y=﹣x2+2mx,以下点可能成为函数顶点的是( )A、(﹣2,4) B、(1,2) C、(﹣1,﹣1) D、(2,﹣4)8. 在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则( )A、C与∠α的大小有关 B、当∠α=45°时,S= C、A,B,C,D四个点可以在同一个圆上 D、S随∠α的增大而增大9. 对于二次函数y=x2﹣2mx+3m﹣3,以下说法:①图象过定点( ),②函数图象与x轴一定有两个交点,③若x=1时与x=2017时函数值相等,则当x=2018时的函数值为﹣3,④当m=﹣1时,直线y=﹣x+1与直线y=x+3关于此二次函数对称轴对称,其中正确命题是( )A、①② B、②③ C、①②④ D、①③④10. 如图,在△ABC中,∠A=36°,AC=AB=2,将△ABC绕点B逆时针方向旋转得到△DBE,使点E在边AC上,DE交AB于点F,则△AFE与△DBF的面积之比等于( )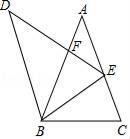 A、
A、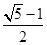 B、
B、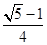 C、
C、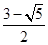 D、
D、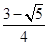
二、填空题
-
11. 已知正n边形的每一个内角为135°,则n= .12. 已知a= ,则(4a+b)2﹣(4a﹣b)2为 .13. 标号分别为1,2,3,4,……,n的n张标签(除标号外其它完全相同),任摸一张,若摸得奇数号标签的概率大于0.5,则n可以是 .14. 在Rt△ABC中,∠ABC=90°,AB=2,BC=1,将△ABC绕AB所在直线旋转一周,得到的几何体的侧面积为 .15. 定义:关于x的函数y=mx2+nx与y=nx2+mx(其中mn≠0)叫做互为交换函数,若这两个函数图象的顶点关于x轴对称,那么m,n满足的关系式为 .16. 已知△ABC与△ABD不全等,且AC=AD=1,∠ABD=∠ABC=45°,∠ACB=60°,则CD= .
三、解答题
-
17. 已知x=﹣3,求代数式(1+ )÷ 的值.18. 如图,BE是△ABC的角平分线,延长BE至D,使得BC=CD.
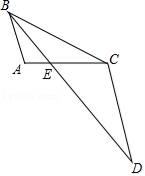 (1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.19. 从数﹣1,0,1,2,3中任取两个,其和的绝对值为k(k是自然数)的概率记作Pk , (如:P2是任取两个数,其和的绝对值为2的概率)(1)、求k的所有取值;(2)、求P3 .20. 二次函数y=(m+1)x2﹣2(m+1)x﹣m+3.(1)、求该二次函数的对称轴;(2)、过动点C(0,n)作直线l⊥y轴,当直线l与抛物线只有一个公共点时,求n关于m的函数表达式;(3)、若对于每一个给定的x值,它所对应的函数值都不大于6,求整数m.21. 已知:在△ABC中,∠A=90°,AB=6,AC=8,点P在边AC上,且⊙P与AB,BC都相切.
(1)、求证:△AEB∽△CED;(2)、若AB=2,BC=4,AE=1,求CE长.19. 从数﹣1,0,1,2,3中任取两个,其和的绝对值为k(k是自然数)的概率记作Pk , (如:P2是任取两个数,其和的绝对值为2的概率)(1)、求k的所有取值;(2)、求P3 .20. 二次函数y=(m+1)x2﹣2(m+1)x﹣m+3.(1)、求该二次函数的对称轴;(2)、过动点C(0,n)作直线l⊥y轴,当直线l与抛物线只有一个公共点时,求n关于m的函数表达式;(3)、若对于每一个给定的x值,它所对应的函数值都不大于6,求整数m.21. 已知:在△ABC中,∠A=90°,AB=6,AC=8,点P在边AC上,且⊙P与AB,BC都相切.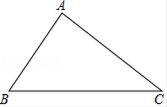 (1)、求⊙P半径;(2)、求sin∠PBC.22. 已知函数y1=x﹣m+1和y2= (n≠0)的图象交于P,Q两点.(1)、若y1的图象过(n,0),且m+n=3,求y2的函数表达式:(2)、若P,Q关于原点成中心对称.
(1)、求⊙P半径;(2)、求sin∠PBC.22. 已知函数y1=x﹣m+1和y2= (n≠0)的图象交于P,Q两点.(1)、若y1的图象过(n,0),且m+n=3,求y2的函数表达式:(2)、若P,Q关于原点成中心对称.①求m的值;
②当x>2时,对于满足条件0<n<n0的一切n总有y1>y2 , 求n0的取值范围.
23. 已知△ABD与△GDF都是等腰直角三角形,BD与DF均为斜边(BD<DF). (1)、如图1,B,D,F在同一直线上,过F作MF⊥GF于点F,取MF=AB,连结AM交BF于点H,连结GA,GM.
(1)、如图1,B,D,F在同一直线上,过F作MF⊥GF于点F,取MF=AB,连结AM交BF于点H,连结GA,GM.①求证:AH=HM;
②请判断△GAM的形状,并给予证明;
③请用等式表示线段AM,BD,DF的数量关系,并说明理由.
(2)、如图2,GD⊥BD,连结BF,取BF的中点H,连结AH并延长交DF于点M,请用等式直接写出线段AM,BD,DF的数量关系.