浙江省杭州市2018届数学中考模拟试卷(6月份)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. ﹣9的绝对值是( )A、﹣9 B、9 C、 D、
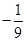 2. 我市今年参加中考人数约为42000人,将42000用科学记数法表示为( )A、4.2×104 B、0.42×105 C、4.2×103 D、42×1033. 在实数范围内,下列判断正确的是( )A、若
2. 我市今年参加中考人数约为42000人,将42000用科学记数法表示为( )A、4.2×104 B、0.42×105 C、4.2×103 D、42×1033. 在实数范围内,下列判断正确的是( )A、若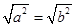 ,则a=b
B、若|a|=( )2 , 则a=b
C、若a>b,则a2>b2
D、若( )2=( )2则a=b
4. 已知数据1、5、4、3、3、2,则下列关于这组数据的说法错误的是( )A、平均数和众数都是3 B、中位数为3 C、方差为10 D、标准差是
,则a=b
B、若|a|=( )2 , 则a=b
C、若a>b,则a2>b2
D、若( )2=( )2则a=b
4. 已知数据1、5、4、3、3、2,则下列关于这组数据的说法错误的是( )A、平均数和众数都是3 B、中位数为3 C、方差为10 D、标准差是 5. 如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则下列说法正确的是( )
5. 如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则下列说法正确的是( )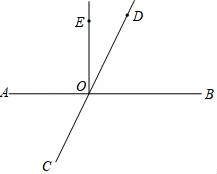 A、∠AOE与∠BOC互为对顶角 B、图中有两个角是∠EOD的邻补角 C、线段DO大于EO的理由是垂线段最短 D、∠AOC=65°6. 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( )
A、∠AOE与∠BOC互为对顶角 B、图中有两个角是∠EOD的邻补角 C、线段DO大于EO的理由是垂线段最短 D、∠AOC=65°6. 如图为某商店的宣传单,小胜到此店同时购买了一件标价为x元的衣服和一条标价为y元的裤子,共节省500元,则根据题意所列方程正确的是( ) A、0.6x+0.4y+100=500 B、0.6x+0.4y﹣100=500 C、0.4x+0.6y+100=500 D、0.4x+0.6y﹣100=5007. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外都相同,其中有5个红球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个黄球的概率为( )A、 B、
A、0.6x+0.4y+100=500 B、0.6x+0.4y﹣100=500 C、0.4x+0.6y+100=500 D、0.4x+0.6y﹣100=5007. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外都相同,其中有5个红球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个黄球的概率为( )A、 B、 C、
D、
8. 如图,点P是矩形ABCD的边上一动点,矩形两边长AB,BC长分别为3和4,那么P到矩形两条对角线AC和BD的距离之和是( )
C、
D、
8. 如图,点P是矩形ABCD的边上一动点,矩形两边长AB,BC长分别为3和4,那么P到矩形两条对角线AC和BD的距离之和是( )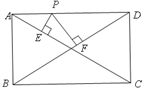 A、
A、 B、
C、
B、
C、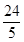 D、不确定
9. 二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中x与y的部分对应值如下表:
D、不确定
9. 二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中x与y的部分对应值如下表:x
﹣2
﹣1
0
1
2
3
4
y
5
0
﹣3
﹣4
﹣3
0
5
给出以下三个结论:(1)二次函数y=ax2+bx+c最小值为﹣4;(2)若y<0,则x的取值范围是0<x<2;(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧,则其中正确结论的个数是( )
A、0 B、1 C、2 D、310. 如图,△ABC,△FGH中,D,E两点分别在AB,AC上,F点在DE上,G、H两点在BC上,且DE∥BC,FG∥AB,FH∥AC,若BG:GH:HC=4:6:5,则△ADE与△FGH的面积比为何?( )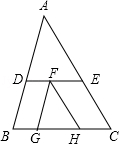 A、2:1 B、3:2 C、5:2 D、9:4
A、2:1 B、3:2 C、5:2 D、9:4二、填空题
-
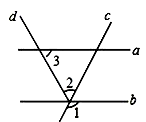
11. 已知单项式3amb2与﹣ a4bn﹣1的和是单项式,那么2m﹣n= .12. 如图,a∥b,∠1=110°,∠3=40°,则∠2=°
 13. 分解因式:9abc-3ac2= .14. 如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= .
13. 分解因式:9abc-3ac2= .14. 如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= .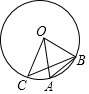 15. 星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是千米.
15. 星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示,则上午8:45小明离家的距离是千米.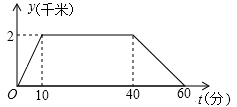 16. 如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为 .
16. 如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为 .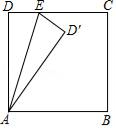
三、解答题
-
17. 家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加 kΩ.
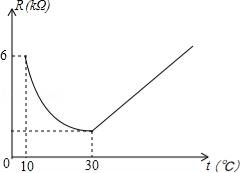 (1)、求R和t之间的关系式;(2)、家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.18. 某校七年级1班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:
(1)、求R和t之间的关系式;(2)、家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.18. 某校七年级1班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:次数
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
频数
a
4
12
16
8
3
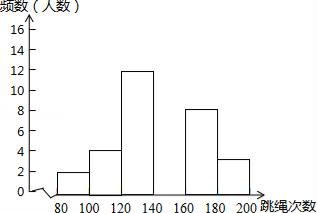
结合图表完成下列问题:
(1)、a=;(2)、补全频数分布直方图;(3)、写出全班人数是 , 并求出第三组“120≤x<140”的频率(精确到0.01)(4)、若跳绳次数不少于140的学生成绩为优秀,则优秀学生人数占全班总人数的百分之几?19. 已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.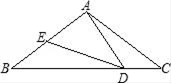 (1)、求证:△BDE∽△CAD;(2)、若CD=2,求BE的长.20. 对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,﹣1}=﹣1,min{2,2}=2.类似地,若函数y1、y2都是x的函数,则y=min{y1 , y2}表示函数y1和y2的“取小函数”.
(1)、求证:△BDE∽△CAD;(2)、若CD=2,求BE的长.20. 对于实数a,b,我们可以用min{a,b}表示a,b两数中较小的数,例如min{3,﹣1}=﹣1,min{2,2}=2.类似地,若函数y1、y2都是x的函数,则y=min{y1 , y2}表示函数y1和y2的“取小函数”.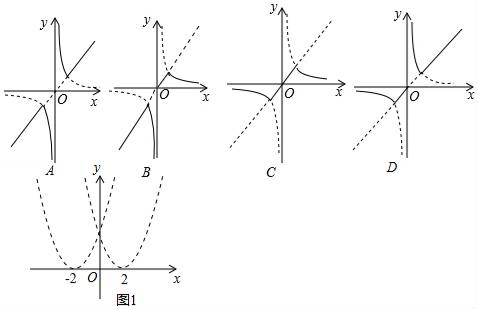 (1)、设y1=x,y2= ,则函数y=min{x, }的图象应该是中的实线部分.(2)、请在图1中用粗实线描出函数y=min{(x﹣2)2 , (x+2)2}的图象 , 并写出该图象的三条不同性质:
(1)、设y1=x,y2= ,则函数y=min{x, }的图象应该是中的实线部分.(2)、请在图1中用粗实线描出函数y=min{(x﹣2)2 , (x+2)2}的图象 , 并写出该图象的三条不同性质:①;②;③;
(3)、函数y=min{(x﹣4)2 , (x+2)2}的图象关于对称.21. 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求: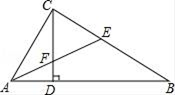 (1)、CD的长;(2)、△ABC的角平分线AE交CD于点F,交BC于E点,求证:∠CFE=∠CEF.22. 如图,抛物线y=ax2+ x+c(a≠0)与x轴交于点A,B两点,其中A(-1,0),与y轴交于点C(0,2).
(1)、CD的长;(2)、△ABC的角平分线AE交CD于点F,交BC于E点,求证:∠CFE=∠CEF.22. 如图,抛物线y=ax2+ x+c(a≠0)与x轴交于点A,B两点,其中A(-1,0),与y轴交于点C(0,2). (1)、求抛物线的表达式及点B坐标;(2)、点E是线段BC上的任意一点(点E与B、C不重合),过点E作平行于y轴的直线交抛物线于点F,交x轴于点G.
(1)、求抛物线的表达式及点B坐标;(2)、点E是线段BC上的任意一点(点E与B、C不重合),过点E作平行于y轴的直线交抛物线于点F,交x轴于点G.①设点E的横坐标为m,用含有m的代数式表示线段EF的长;
②线段EF长的最大值是 .
23. 阅读下列材料,完成任务:自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
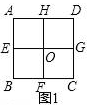
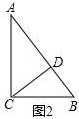
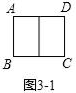
 (1)、图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为;(2)、如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为;(3)、现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
(1)、图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为;(2)、如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为;(3)、现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).请从下列A、B两题中任选一条作答:我选择题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a=(用含b的式子表示);
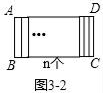
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a=(用含n,b的式子表示);
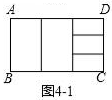
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a=(用含b的式子表示);
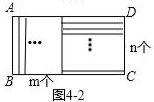
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a=(用含m,n,b的式子表示).