云南省曲靖市2018届数学中考模拟试卷
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 某种品牌的洗面奶,外包装标明净含量为500±10g,表明了这种洗面奶的净含量x的范围是( )A、490<x<510 B、490≤x≤510 C、490<x≤510 D、490≤x<5102. 下列各式计算正确的是( )A、a+2a=3a2 B、(﹣a3)2=a6 C、a3a2=a6 D、(a+b)2=a2+b23. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
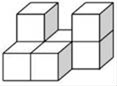 A、主视图 B、俯视图 C、左视图 D、一样大4. 把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )
A、主视图 B、俯视图 C、左视图 D、一样大4. 把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( ) A、6→3 B、7→16 C、7→8 D、6→155. 2017年底我市有绿化面积300公顷,为响应“退耕还林”的号召,计划到2019年底绿化面积增加到363公顷.设绿化面积平均每年的增长率为x,由题意可列方程为( )A、 300(1+x)=363 B、300(1+x)2=363 C、300(1+2x)=363 D、300(1﹣x)2=3636. 不等式组 的解集在数轴上表示正确的是( )A、
A、6→3 B、7→16 C、7→8 D、6→155. 2017年底我市有绿化面积300公顷,为响应“退耕还林”的号召,计划到2019年底绿化面积增加到363公顷.设绿化面积平均每年的增长率为x,由题意可列方程为( )A、 300(1+x)=363 B、300(1+x)2=363 C、300(1+2x)=363 D、300(1﹣x)2=3636. 不等式组 的解集在数轴上表示正确的是( )A、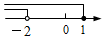 B、
B、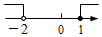 C、
C、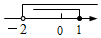 D、
D、 7. 已知△ABC如图1,嘉淇同学进行如下作图(如图2):
7. 已知△ABC如图1,嘉淇同学进行如下作图(如图2):( 1 )分别以点B,C为圆心,AC,AB长为半径作弧,两弧相交于P点;(2)作直线AP,AP与BC交于D点,则线段AD就是△ABC的( )
 A、中线 B、角平分线 C、高线 D、中位线8. 函数y= 的自变量x的取值范围是 .
A、中线 B、角平分线 C、高线 D、中位线8. 函数y= 的自变量x的取值范围是 .二、填空题
-
9. 某种计算机每秒运算次数是4.66亿次,4.66亿次精确到位,4.66亿次用科学记数法可以表示为次.10. 如图,在平面直角坐标系中,直线y=﹣x+3与x轴,y轴交于A,B两点,分别以点A,B为圆心,大于 AB长为半径作圆弧,两弧在第一象限交于点C,若点C的坐标为(m+1,7﹣m),则m的值是 .
 11. 同一个圆的内接正方形和正三角形的边心距的比为 .12. 如果关于x的一元二次方程x2+2x﹣a=0没有实数根,那么a的取值范围是 .13. 有一个数值转换器,原理如图所示,若开始输入x的值是3,可发现第1次输出的结果是10,第2次输出的结果是5,第3次输出的结果是16,第4次输出的结果是8,依次继续下去…,第2018次输出的结果是 .
11. 同一个圆的内接正方形和正三角形的边心距的比为 .12. 如果关于x的一元二次方程x2+2x﹣a=0没有实数根,那么a的取值范围是 .13. 有一个数值转换器,原理如图所示,若开始输入x的值是3,可发现第1次输出的结果是10,第2次输出的结果是5,第3次输出的结果是16,第4次输出的结果是8,依次继续下去…,第2018次输出的结果是 .
三、解答题
-
14. 计算:(1)、( )2﹣ ﹣(2)、(3)、|﹣3|+(π+1)0(4)、( )× .15. 某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型
频数
频率
跳绳
25
a
实心球
20
50m
b
0.4
拔河
0.15
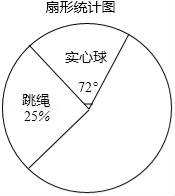
(1)、直接写出a= , b=;(2)、将图中的扇形统计图补充完整(注明项目、百分比);(3)、若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?
16. 列方程解应用题:某城市为了治理污水,需要铺设一条全长为3000米的污水排放管道.为使工程提前10天完成,在保证质量的前提下,必须把工作效率提高25%.问原计划每天铺设管道多少米?
17. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D,且B(3,﹣1),求:
(Ⅰ)求反比例函数的解析式;
(Ⅱ)求点D坐标,并直接写出y1>y2时x的取值范围;
(Ⅲ)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
18. 一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.(1)、若从中任取一个球,球上的汉字刚好是 “书”的概率为.(2)、从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.19. 已知,如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.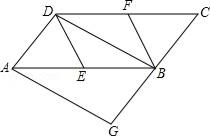 (1)、求证:四边形AGBD为平行四边形;(2)、若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?证明你的结论.20. 如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)、求证:四边形AGBD为平行四边形;(2)、若四边形AGBD是矩形,则四边形BEDF是什么特殊四边形?证明你的结论.20. 如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E. (1)、求证:直线EC为圆O的切线;(2)、设BE与圆O交于点F,AF的延长线与CE交于点P,已知∠PCF=∠CBF,PC=5,PF=4,求sin∠PEF的值.21. 如图1,在平面直角坐标系xOy中,直线l: 与x轴、y轴分别交于点A和点B(0,﹣1),抛物线 经过点B,且与直线l的另一个交点为C(4,n).
(1)、求证:直线EC为圆O的切线;(2)、设BE与圆O交于点F,AF的延长线与CE交于点P,已知∠PCF=∠CBF,PC=5,PF=4,求sin∠PEF的值.21. 如图1,在平面直角坐标系xOy中,直线l: 与x轴、y轴分别交于点A和点B(0,﹣1),抛物线 经过点B,且与直线l的另一个交点为C(4,n).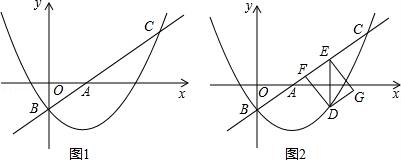 (1)、求n的值和抛物线的解析式;(2)、点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)、M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1 , 点A、O、B的对应点分别是点A1、O1、B1 . 若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.
(1)、求n的值和抛物线的解析式;(2)、点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)、M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1 , 点A、O、B的对应点分别是点A1、O1、B1 . 若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.