云南省红河州弥勒市2018届数学中考二模试卷

试卷更新日期：2019-03-06 类型：中考模拟

进入出卷网下载

一、单选题

1. 人体中红细胞的直径约为0.0000077m，将数0.0000077用科学记数法表示为（）

A、77×10^﹣⁵ B、0.77×10^﹣⁷ C、7.7×10^﹣⁶ D、7.7×10^﹣⁷

查看试题解析
2. 右图是某个几何体的三视图，该几何体是（）

A、圆锥 B、三棱锥 C、圆柱 D、三棱柱

查看试题解析
3. 下列运算正确的是（）

A、3x+2y=5xy B、（m²）³=m⁵ C、（a+1）（a﹣1）=a²﹣1 D、 =2

查看试题解析
4. 下列图案属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5.
公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m² ，求原正方形空地的边长．设原正方形的空地的边长为xm，则可列方程为（）

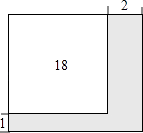A、（x+1）（x+2）=18 B、x²﹣3x+16=0 C、（x﹣1）（x﹣2）=18 D、x²+3x+16=0

查看试题解析
6. 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（）

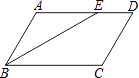A、150° B、130° C、120° D、100°

查看试题解析
7. 如图，点A是反比例函数 $y = - \frac{6}{x}$ （x＜0）的图象上的一点，过点A作平行四边形ABCD，使B，C在x轴上，点D在y轴上，则平行四边形ABCD的面积为（）

A、1 B、3 C、6 D、12

查看试题解析
8. 如图，在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是 $\overset{⌢}{A B}$ 的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2 $\sqrt{2}$ 时，则阴影部分的面积为（）

A、2π﹣4 B、4π﹣8 C、2π﹣8 D、4π﹣4

查看试题解析

二、填空题

9. 化简： $\sqrt{8} - \sqrt{2}$ = ．

查看试题解析
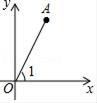
10. 因式分解：2a² – 8 = ．

查看试题解析
11. 若一元二次方程 $x^{2} + 4 x + c = 0$ 有两个不相等的实数根，则c的值可以是（写出一个即可）.

查看试题解析
12. 如图，若点A的坐标为（1， $\sqrt{3}$ ），则∠1= ， sin∠1= ．

查看试题解析
13. 小明随机调查了本班5名同学的家庭一个月的平均用水量（单位：t），记录如下：9，11，8，6，15，则这组数据的中位数是．

查看试题解析
14. 观察下列图形：

它们是按一定的规律排列，依照此规律第n个图形共有个．

查看试题解析

三、解答题

15. 计算：|﹣ $\frac{1}{3}$ |+（π﹣2017）⁰﹣2sin30°+3^﹣¹ ．

查看试题解析
16. 已知：如图所示△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连接AE，BD．求证：AE=BD．

查看试题解析
17. 某校为了解本校九年级男生“引体向上”项目的训练情况，随机抽取该年级部分男生进行了一次测试（满分15分，成绩均记为整数分），并按测试成绩（单位：分）分成四类：A类（12≤m≤15），B类（9≤m≤11），C类（6≤m≤8），D类（m≤5）绘制出以下两幅不完整的统计图，请根据图中信息解答下列问题：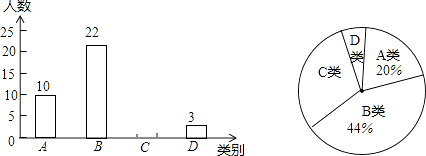

(1)、本次抽取样本容量为，扇形统计图中A类所对的圆心角是度；

(2)、请补全统计图；

(3)、若该校九年级男生有300名，请估计该校九年级男生“引体向上”项目成绩为C类的有多少名？

查看试题解析
18. 如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图．已知长方体货厢的高度BC为 $\sqrt{5}$ 米，tanA= $\frac{1}{3}$ ．现把图中的货物继续往前平移，当货物顶点D与C重合时，仍可把货物放平装进货厢，求BD的长．（结果保留根号）

查看试题解析
19. 在“母亲节”前期，某花店购进康乃馨和玫瑰两种鲜花，销售过程中发现康乃馨比玫瑰销售量大，店主决定将玫瑰每枝降价1元促销，降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍．

(1)、求降价后每枝玫瑰的售价是多少元？

(2)、根据销售情况，店主用不多于900元的资金再次购进两种鲜花共500枝，康乃馨进价为2元/枝，玫瑰进价为1.5元/枝，问至少购进玫瑰多少枝？

查看试题解析
20.
如图，直线y=x+2与抛物线y=ax²+bx+6（a≠0）相交于A（ $\frac{1}{2}$ ， $\frac{5}{2}$ ）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．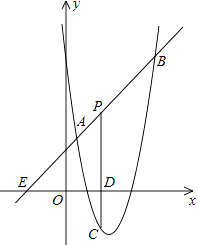

(1)、求抛物线的解析式；

(2)、是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．

查看试题解析
21. 如图，在△ABC中，AB=AC，以AB为直径的⊙O与边BC，AC分别交于D，E两点，过点D作DH⊥AC于点H．

(1)、判断DH与⊙O的位置关系，并说明理由；

(2)、求证：H为CE的中点；

(3)、若BC=10，cosC= $\frac{\sqrt{5}}{5}$ ，求AE的长．

查看试题解析
22. 在 $△ A B C$ 中， $A B = B C = 2 ， ∠ A B C = 120 °$ 将 $△ A B C$ 绕点 $B$ 顺时针旋转角 $α$ $(0 ° <$ $α$ $< 90 °)$ 得 $△ A_{1} B C_{1} ， A_{1} B$ 交 $A C$ 于点 $E$ ， $A_{1} C_{1}$ 分别交 $A C 、 B C$ 于 $D 、 F$ 两点．

(1)、如图1，观察并猜想，在旋转过程中，线段 ${EA}_{1}$ 与 $F C$ 有怎样的数量关系？并证明你的结论；

(2)、如图2，当 $α$ = $30 °$ 时，试判断四边形 ${BC}_{1} DA$ 的形状，并说明理由；

(3)、在（2）的情况下，求 $ED$ 的长．

查看试题解析