云南省红河州蒙自市2018届数学中考模拟试卷（4月份）

试卷更新日期：2019-03-06 类型：中考模拟

进入出卷网下载

一、单选题

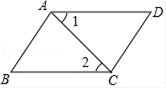
1. 某种病毒近似于球体，它的半径约为0.000000005米，用科学记数法表示为（）

A、5×10⁸ B、5×10⁹ C、5×10^﹣8 D、5×10^﹣9

查看试题解析
2. 如图，AB∥CD，那么（）

A、∠BAD与∠B互补 B、∠1=∠2 C、∠BAD与∠D互补 D、∠BCD与∠D互补

查看试题解析
3. 下列运算或变形正确的是（）

A、﹣2a+2b=﹣2（a+b） B、a²﹣2a+4=（a﹣2）² C、（2a²）³=6a⁶ D、3a²•2a³=6a⁵

查看试题解析
4. 反比例函数y= $\frac{1}{x}$ 的图象向右平移 $\sqrt{2015}$ 个单位长度得到一个新的函数，当自变量x取1，2，3，4，5，…，（正整数）时，新的函数值分别为y₁ ， y₂ ， y₃ ， y₄ ， y₅ ， …，其中最小值和最大值分别为（）

A、y₁ ， y₂ B、y₄₃ ， y₄₄ C、y₄₄ ， y₄₅ D、y₂₀₁₄ ， y₂₀₁₅

查看试题解析
5. 有以下图形：平行四边形、矩形、等腰三角形、线段、菱形，其中既是轴对称图形又是中心对称图形的有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

6. 某校八年级两个班，各选派10名学生参加学校举行的“古诗词”大赛，各参赛选手成绩的数据分析如表所示，则以下判断错误的是（）

班级	平均数	中位数	众数	方差
八（1）班	94	93	94	12
八（2）班	95	95.5	93	8.4

A、八（2）班的总分高于八（1）班 B、八（2）班的成绩比八（1）班稳定 C、两个班的最高分在八（2）班 D、八（2）班的成绩集中在中上游

查看试题解析

7. 已知⊙O的半径为10，P为⊙O内一点，且OP=6，则过P点，且长度为整数的弦有（）

A、5条 B、6条 C、8条 D、10条

查看试题解析
8. 二维码已经给我们的生活带来了很大方便，它是由大小相同的黑白两色的小正方形（如图1中C）按某种规律组成的一个大正方形，现有25×25格式的正方形如图1，角上是三个7×7的A型大黑白相间正方形，中间右下一个5×5的B型黑白相间正方形，除这4个正方形外，若其他的小正方形白色块数y与黑色块数x正好满足如图2所示的函数图象，则该25×25格式的二维码共有多少块黑色的C型小正方形（）

A、153 B、218 C、100 D、216

查看试题解析

二、填空题

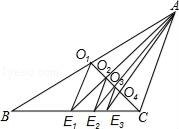
9. 结合具体的数，通过特例进行归纳，判断“如果a大于b，那么a的倒数小于b的倒数”，这句话的对错，你给出的特例是：a= ， b= ．你认为（填“对”或“错”）．

查看试题解析
10. 若不等式组 ${\begin{matrix} x < 4 \\ x < m \end{matrix}$ 的解集是x＜4，则m的取值范围是．

查看试题解析
11. 如图，已知CO₁是△ABC的中线，过点O₁作O₁E₁∥AC交BC于点E₁ ，连接AE₁交CO₁于点O₂；过点O₂作O₂E₂∥AC交BC于点E₂ ，连接AE₂交CO₁于点O₃；过点O₃作O₃E₃∥AC交BC于点E₃ ， …，如此继续，可以依次得到点O₄ ， O₅ ， …，O_n和点E₄ ， E₅ ， …，E_n ，则O₂₀₁₆E₂₀₁₆=AC．

查看试题解析
12. 已知函数 $y = \sqrt{x - 2}$ ，则x取值范围是．

查看试题解析
13. 一个几何体的三视图如图，很据图示的数据计算该几何体的表面积为（结果保留π）．

查看试题解析
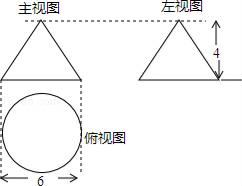14. 如图，函数y=kx+b的图象与x轴，y轴分别交于A（﹣2，0），B（0，1）两点，那么此函数的图象与函数y=x﹣1的图象交点C的坐标是．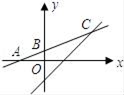

查看试题解析

三、解答题

15. 计算：（ $\sqrt{3}$ ﹣2）⁰+ ${(\frac{1}{3})}^{- 1}$ +4cos30°﹣|﹣ $\sqrt{12}$ |．

查看试题解析
16. 如图所示，一个四边形纸片ABCD，∠B=∠D=90°，把纸片按如图所示折叠，使点B落在AD边上的B′点，AE是折痕．

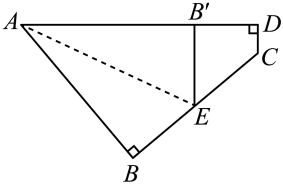(1)、试判断B′E与DC的位置关系；

(2)、如果∠C=130°，求∠AEB的度数．

查看试题解析
17. 随着中国传统节日“端午节”的临近，东方红商场决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折，已知打折前，买6盒甲品牌粽子和3盒乙品牌粽子需660元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．

(1)、打折前甲、乙两种品牌粽子每盒分别为多少元？

(2)、阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？

查看试题解析
18. 学习习近平总书记关于生态文明建设重要井话，牢固树立“绿水青山就是金山银山”的科学观，让环保理念深入到学校，某校张老师为了了解本班学生3月植树成活情况，对本班全体学生进行了调查，并将调查结果分为了三类：A好，B：中，C：差．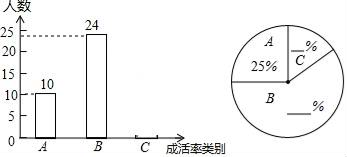

请根据图中信息，解答下列问题：

(1)、求全班学生总人数；

(2)、将上面的条形统计图与扇形统计图补充完整；

(3)、张老师在班上随机抽取了4名学生，其中A类1人，B类2人，C类1人，若再从这4人中随加抽取2人，请用画对状图或列表法求出全是B类学生的概率．

查看试题解析
19. 在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．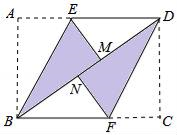

(1)、求证：四边形BFDE为平行四边形；

(2)、若四边形BFDE为菱形，且AB=3，求BC的长．

查看试题解析
20. 填空： $\frac{1}{2}$ =1﹣ $\frac{1}{2}$ ， $\frac{1}{6}$ = $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ， $\frac{1}{12}$ = $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ， $\frac{1}{20}$ = $\frac{1}{4}$ ﹣ $\frac{1}{5}$ ，…．

(1)、试求 $\frac{1}{30}$ = ， $\frac{1}{42}$ = ．

(2)、请猜想能表示上述规律的等式，并用含字母n（n 整数）的式子表示出来

(3)、请你直接利用（2）所得的结论计算下列式子：
$\frac{1}{x (x + 1)} + \frac{1}{(x + 1) (x + 2)} + \frac{1}{(x + 2) (x + 3)} + \dots + \frac{1}{(x + 2008) (x + 2009)}$ ．

查看试题解析
21. 如图，AB为⊙O的直径，CD切⊙O于点C，与BA的延长线交于点D，OE⊥AB交⊙O于点E，连接CA、CE、CB，CE交AB于点G，过点A作AF⊥CE于点F，延长AF交BC于点P．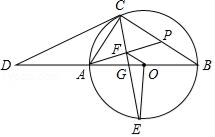

（Ⅰ）求∠CPA的度数；

（Ⅱ）连接OF，若AC= $\sqrt{3}$ ，∠D=30°，求线段OF的长．

查看试题解析
22. 如图1，在平面直角坐标系xOy中，直线l： $y = \frac{3}{4} x + π$ 与x轴、y轴分别交于点A和点B（0，﹣1），抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点B，且与直线l的另一个交点为C（4，n）．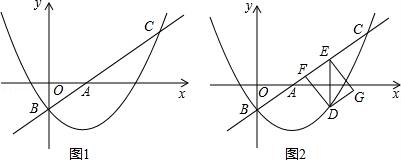

(1)、求n的值和抛物线的解析式；

(2)、点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；

(3)、M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A₁O₁B₁ ，点A、O、B的对应点分别是点A₁、O₁、B₁ ．若△A₁O₁B₁的两个顶点恰好落在抛物线上，请直接写出点A₁的横坐标．

查看试题解析