云南省红河州开远市2018届数学中考模拟试卷
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 计算1+2+22+23+…+22010的结果是( )A、22011﹣1 B、22011+1 C、
 D、
D、 2. 我市今年参加中考人数约为42000人,将42000用科学记数法表示为( )A、4.2×104 B、0.42×105 C、4.2×103 D、42×1033. 如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是( )
2. 我市今年参加中考人数约为42000人,将42000用科学记数法表示为( )A、4.2×104 B、0.42×105 C、4.2×103 D、42×1033. 如图,在下列四个几何体中,从正面、左面、上面看不完全相同的是( )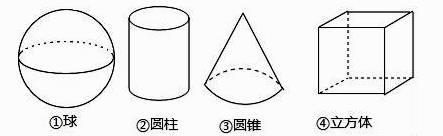 A、①② B、②③ C、①④ D、②④4. 某青年排球队12名队员的年龄情况如表:
A、①② B、②③ C、①④ D、②④4. 某青年排球队12名队员的年龄情况如表:年龄
18
19
20
21
22
人数
1
4
3
2
2
则这个队队员年龄的众数和中位数是( )
A、19,20 B、19,19 C、19,20.5 D、20,195. 如果a﹣b=5,那么代数式( ﹣2)• 的值是( )A、﹣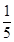 B、
B、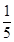 C、﹣5
D、5
6. 解不等式 ,解题依据错误的是( )
C、﹣5
D、5
6. 解不等式 ,解题依据错误的是( )解:①去分母,得5(x+2)<3(2x﹣1)②去括号,得5x+10<6x﹣3③移项,得5x﹣6x<﹣3﹣10④合并同类项,得﹣x<﹣13⑤系数化1,得x>13
A、②去括号法则 B、③不等式的基本性质1 C、④合并同类项法则 D、⑤不等式的基本性质27. 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为E,点P在⊙O上,连接BP,PD,BC.若CD= ,sinP= ,则⊙O的直径为( )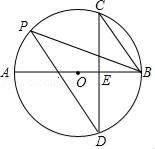 A、8 B、6 C、5 D、
A、8 B、6 C、5 D、 8. 如图①,在边长为2cm的正方形ABCD中,点P以每秒1cm的速度从点A出发,沿AB→BC的路径运动,到点C停止,过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动3秒时,PQ的长是( )
8. 如图①,在边长为2cm的正方形ABCD中,点P以每秒1cm的速度从点A出发,沿AB→BC的路径运动,到点C停止,过点P作PQ∥BD,PQ与边AD(或边CD)交于点Q,PQ的长度y(cm)与点P的运动时间x(秒)的函数图象如图②所示.当点P运动3秒时,PQ的长是( )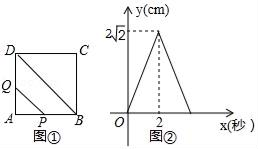 A、
A、 cm
B、
cm
B、 cm
C、
cm
C、 cm
D、
cm
D、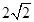 cm
cm
二、填空题
-
9. m为负整数,则m与它的倒数 之间的大小关系是m .10. 若u、v满足v= ,则u2﹣uv+v2= .11. 如图,AB∥CD,CE与AB交于点A,BE⊥CE,垂足为E.若∠C=37°,则∠B=.
 12. 如图,分别以正六边形相间隔的3个顶点为圆心,以这个正六边形的边长为半径作扇形得到 “三叶草”图案,若正六边形的边长为3,则“三叶草”图案中阴影部分的面积为(结果保留π)
12. 如图,分别以正六边形相间隔的3个顶点为圆心,以这个正六边形的边长为半径作扇形得到 “三叶草”图案,若正六边形的边长为3,则“三叶草”图案中阴影部分的面积为(结果保留π) 13. 如图,已知动点A在函数y= (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于 .
13. 如图,已知动点A在函数y= (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于 .
三、解答题
-
14. 如图,在⊙O中, ,∠1=45°,求∠2的度数.
 15. 阅读材料:
15. 阅读材料:小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
 (1)、请按照小明的思路完成上述问题:求每个小长方形的面积;(2)、某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是cm;(3)、小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.16. 停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
(1)、请按照小明的思路完成上述问题:求每个小长方形的面积;(2)、某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是cm;(3)、小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.16. 停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84) 17. 在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,把球上的数字记为x,再从乙袋中任意摸出一个小球,把球上的数字记为y,以此确定点M的坐标(x,y).(1)、请你用画树状图或列表的方法(只选其中一种),写出点M所有可能的坐标;(2)、求点M(x,y)在函数y=﹣2x的图象上的概率.18. 为提高三亚市初级中学教师业务水平,相关单位举办了首届“三亚市敏特杯数学命题大赛”,在众多自命题题目中共有5道题目进入专家组评审,将前5天的投票数据整理成如下不完整的统计图表:
17. 在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2,乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,把球上的数字记为x,再从乙袋中任意摸出一个小球,把球上的数字记为y,以此确定点M的坐标(x,y).(1)、请你用画树状图或列表的方法(只选其中一种),写出点M所有可能的坐标;(2)、求点M(x,y)在函数y=﹣2x的图象上的概率.18. 为提高三亚市初级中学教师业务水平,相关单位举办了首届“三亚市敏特杯数学命题大赛”,在众多自命题题目中共有5道题目进入专家组评审,将前5天的投票数据整理成如下不完整的统计图表:票数条形统计图
题目编号
人数
百分比
1
40
10%
2
120
m%
3
88
22%
4
a
20%
5
72
18%
合计
400
1

请根据图表提供的信息,解答下面问题:
(1)、票数统计表中的a= , m= .(2)、请把票数统计图补充完整;(3)、若绘制“票数扇形统计图”编号是“4”的题目所对应扇形的圆心角是度;(4)、至本次投票结束,总票数共有1200票,请估计编号是“3”的题目约获得票.19. 已知:如图,在矩形ABCD中,E是BC边一点,DE平分∠ADC,EF∥DC角AD边于点F,连结BD. (1)、求证:四边形EFCD是正方形;(2)、若BE=1,ED=2 ,求BD的长.20. 某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.(1)、降价前商品每月销售该商品的利润是多少元?(2)、要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?(3)、当这种商品售价定为多少元时,该商品所获的利润最大?最大利润是多少?21. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与
(1)、求证:四边形EFCD是正方形;(2)、若BE=1,ED=2 ,求BD的长.20. 某商场以每件280元的价格购进一批商品,当每件商品售价为360元时,每月可售出60件,为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每月就可以多售出5件.(1)、降价前商品每月销售该商品的利润是多少元?(2)、要使商场每月销售这种商品的利润达到7200元,且更有利于减少库存,则每件商品应降价多少元?(3)、当这种商品售价定为多少元时,该商品所获的利润最大?最大利润是多少?21. 如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与OD的延长线交于点P,PC、AB的延长线交于点F.
 (1)、求证:PC是⊙O的切线;(2)、若∠ABC=60°,AB=10,求线段CF的长.22. 已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)、求证:PC是⊙O的切线;(2)、若∠ABC=60°,AB=10,求线段CF的长.22. 已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x. (1)、用含x的代数式表示线段CF的长;(2)、如果把△CAE的周长记作C△CAE , △BAF的周长记作C△BAF , 设 =y,求y关于x的函数关系式,并写出它的定义域;(3)、当∠ABE的正切值是 时,求AB的长.
(1)、用含x的代数式表示线段CF的长;(2)、如果把△CAE的周长记作C△CAE , △BAF的周长记作C△BAF , 设 =y,求y关于x的函数关系式,并写出它的定义域;(3)、当∠ABE的正切值是 时,求AB的长.