云南省2019届九年级数学学业水平考试-几何综合检测
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个多边形的每个内角都等于120°,则这个多边形的边数为( )A、4 B、5 C、6 D、73. 如图是用八块相同的小正方体搭建的几何体,它的左视图是( )
2. 一个多边形的每个内角都等于120°,则这个多边形的边数为( )A、4 B、5 C、6 D、73. 如图是用八块相同的小正方体搭建的几何体,它的左视图是( )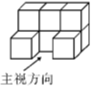 A、
A、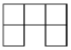 B、
B、 C、
C、 D、
D、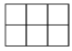 4. 在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于 ( )A、 B、 C、 D、5. 如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( )
4. 在Rt△ABC中,∠C=90°,AB=10,AC=8,则sinA等于 ( )A、 B、 C、 D、5. 如图,OP是∠AOB的平分线,点C,D分别在角的两边OA,OB上,添加下列条件,不能判定△POC≌△POD的选项是( ) A、PC⊥OA,PD⊥OB B、OC=OD C、∠OPC=∠OPD D、PC=PD6. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )
A、PC⊥OA,PD⊥OB B、OC=OD C、∠OPC=∠OPD D、PC=PD6. 如图,AB是⊙O的弦,半径OC⊥AB于点D,若⊙O的半径为5,AB=8,则CD的长是( )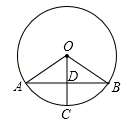 A、2 B、3 C、4 D、57. 如图,在边长为 的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )
A、2 B、3 C、4 D、57. 如图,在边长为 的等边三角形ABC中,过点C垂直于BC的直线交∠ABC的平分线于点P,则点P到边AB所在直线的距离为( )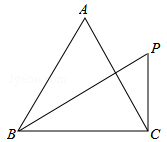 A、 B、 C、 D、18. 如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
A、 B、 C、 D、18. 如图,已知△ABC,AB=AC,将△ABC沿边BC翻转,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )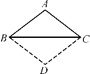 A、四条边相等的四边形是菱形 B、一组邻边相等的平行四边形是菱形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直平分的四边形是菱形
A、四条边相等的四边形是菱形 B、一组邻边相等的平行四边形是菱形 C、对角线互相垂直的平行四边形是菱形 D、对角线互相垂直平分的四边形是菱形二、填空题
-
9. 如图,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD=°.
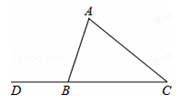 10. 如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE= .
10. 如图,在Rt△ABC中,E是斜边AB的中点,若AB=10,则CE= . 11. 如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是(写出一个即可).
11. 如图,在四边形ABCD中,对角线AC,BD交于点O,OA=OC,OB=OD,添加一个条件使四边形ABCD是菱形,那么所添加的条件可以是(写出一个即可). 12. 如图,AD∥BE∥CF,直线l1 , l2与这三条平行线分别交于点A,B,C和点D,E,F, ,DE=6,则EF= .
12. 如图,AD∥BE∥CF,直线l1 , l2与这三条平行线分别交于点A,B,C和点D,E,F, ,DE=6,则EF= .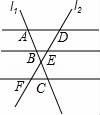 13. 如图,圆锥底面半径为r cm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为 .
13. 如图,圆锥底面半径为r cm,母线长为10cm,其侧面展开图是圆心角为216°的扇形,则r的值为 .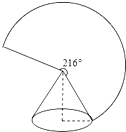 14. 如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2 +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为 .
14. 如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2 +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为 . 15. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
15. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.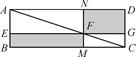
(以上材料来源于《古证复原的原则》《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据上图完成这个推论的证明过程.
证明:S矩形NFGD=S△ADC-(S△ANF+S△FGC),
S矩形EBMF=S△ABC-(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF.
三、解答题
-
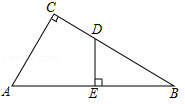
16. 如图,Rt△ABC中,∠C=90°,AB=14,AC=7,D是BC上一点,BD=8,DE⊥AB,垂足为E,求线段DE的长.
 17. 如图,△ABC,△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,求证:△CDA≌△CEB.
17. 如图,△ABC,△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,点E在AB上,求证:△CDA≌△CEB.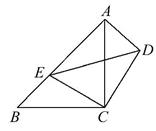 18. 已知点E是矩形ABCD的边CD上一点,BF⊥AE于点F,求证△ABF∽△EAD.
18. 已知点E是矩形ABCD的边CD上一点,BF⊥AE于点F,求证△ABF∽△EAD.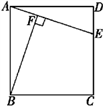 19. 如图,在△ABC中,AB=AC=1,BC= ,在AC边上截取AD=BC,连接BD.
19. 如图,在△ABC中,AB=AC=1,BC= ,在AC边上截取AD=BC,连接BD.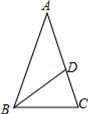 (1)、通过计算,判断AD2与AC•CD的大小关系;(2)、求∠ABD的度数.20. 用如图所示矩形纸片的四个角都剪去一个边长为 的正方形(阴影部分).并制成一个长方体纸盒。
(1)、通过计算,判断AD2与AC•CD的大小关系;(2)、求∠ABD的度数.20. 用如图所示矩形纸片的四个角都剪去一个边长为 的正方形(阴影部分).并制成一个长方体纸盒。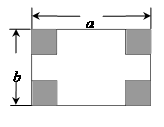 (1)、用a,b,x表示纸片剩余部分的面积和纸盒的底面积;(2)、当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.21. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上
(1)、用a,b,x表示纸片剩余部分的面积和纸盒的底面积;(2)、当a=6,b=4,且剪去部分的面积等于剩余部分的面积时,求正方形的边长.21. 如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上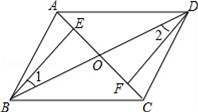 (1)、给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)、在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.22. 如图,Rt△ABC中,∠C=90°,AC= ,tanB= ,半径为2的⊙C,分别交AC,BC于点D,E,得到 .
(1)、给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)、在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.22. 如图,Rt△ABC中,∠C=90°,AC= ,tanB= ,半径为2的⊙C,分别交AC,BC于点D,E,得到 .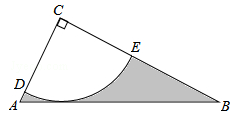 (1)、求证:AB为⊙C的切线;(2)、求图中阴影部分的面积.23. 如图,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE∶CE=3∶2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)、求证:AB为⊙C的切线;(2)、求图中阴影部分的面积.23. 如图,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE∶CE=3∶2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.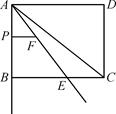 (1)、线段AE=;(2)、设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;(3)、当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径.
(1)、线段AE=;(2)、设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;(3)、当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径.