广西钦州市2018届数学中考模拟试卷(4月份)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 两个有理数的和为零,则这两个数一定是( )A、都是零 B、至少有一个是零 C、一个是正数,一个是负数 D、互为相反数2. 2017年,全国参加汉语考试的人数约为6500000,将6500000用科学记数法表示为( )A、 6.5×105 B、6.5×106 C、6.5×107 D、65×1053. 下列几何体是棱锥的是( )A、
 B、
B、 C、
C、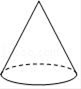 D、
D、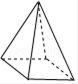 4. 不等式3x<2(x+2)的解是( )A、x>2 B、x<2 C、x>4 D、x<45. 如果将一副三角板按如图方式叠放,那么∠1等于( )
4. 不等式3x<2(x+2)的解是( )A、x>2 B、x<2 C、x>4 D、x<45. 如果将一副三角板按如图方式叠放,那么∠1等于( )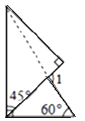 A、120° B、105° C、60° D、45°6. 已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、不能确定7. 等腰三角形的两边长分别为5和11,则它的周长为( )A、21 B、21或27 C、27 D、258. 一个两位数,它的十位数字是3,个位数字是抛掷一枚质地均匀的骰子(六个面分别标有数字1﹣6)朝上一面的数字,任意抛掷这枚骰子一次,得到的两位数是3的倍数的概率等于( )A、 B、 C、 D、9. 若α,β是一元二次方程3x2+2x-9=0的两根,则 的值是( ).A、
A、120° B、105° C、60° D、45°6. 已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、不能确定7. 等腰三角形的两边长分别为5和11,则它的周长为( )A、21 B、21或27 C、27 D、258. 一个两位数,它的十位数字是3,个位数字是抛掷一枚质地均匀的骰子(六个面分别标有数字1﹣6)朝上一面的数字,任意抛掷这枚骰子一次,得到的两位数是3的倍数的概率等于( )A、 B、 C、 D、9. 若α,β是一元二次方程3x2+2x-9=0的两根,则 的值是( ).A、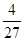 B、-
B、- 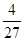 C、-
C、- 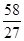 D、
D、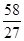 10. 下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )A、
10. 下列四个函数图象中,当x<0时,函数值y随自变量x的增大而减小的是( )A、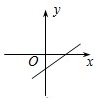 B、
B、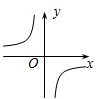 C、
C、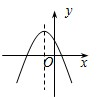 D、
D、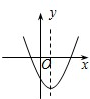 11. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
11. 如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( ) A、8 B、8 C、4 D、612. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y= (x>0)的图象上,若AB=2,则k的值为( )
A、8 B、8 C、4 D、612. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y= (x>0)的图象上,若AB=2,则k的值为( )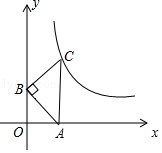 A、4 B、2 C、2 D、
A、4 B、2 C、2 D、二、填空题
-
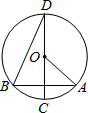
13. 如果一个正多边形的中心角为72°,那么这个正多边形的边数是 .14. 某招聘考试分笔试和面试两项,其中笔试按60%、面试按40%计算加权平均数,作为总成绩,李红笔试成绩为90分,面试成绩为85分,那么李红的总成绩是分.15. 分解因式:2x2﹣8x+8= .16. 如图,⊙O的直径CD垂直于AB,∠AOC=48°,则∠BDC=度.
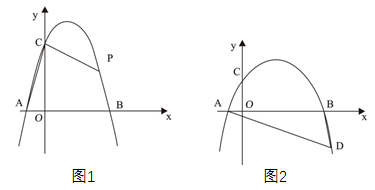
 17. 如图,一次函数y1=kx+b的图象与反比例函数y2= (x<0)的图象相交于点A和点B.当y1>y2>0时,x的取值范围是 .
17. 如图,一次函数y1=kx+b的图象与反比例函数y2= (x<0)的图象相交于点A和点B.当y1>y2>0时,x的取值范围是 .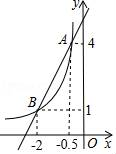 18. 在平面直角坐标系中,智多星做走棋的游戏,其走法是:棋子从原点出发,第1步向上走1个单位,第2步向上走2个单位,第3步向右走1个单位,第4步向上走1个单位……依此类推,第n步的走法是:当n被3除,余数为2时,则向上走2个单位;当走完第2018步时,棋子所处位置的坐标是
18. 在平面直角坐标系中,智多星做走棋的游戏,其走法是:棋子从原点出发,第1步向上走1个单位,第2步向上走2个单位,第3步向右走1个单位,第4步向上走1个单位……依此类推,第n步的走法是:当n被3除,余数为2时,则向上走2个单位;当走完第2018步时,棋子所处位置的坐标是三、解答题
-
19. 计算:( )﹣2﹣ +( ﹣4)0﹣ cos45°.20. 如图,在矩形ABCD中,对角线AC、BD相交于点O.
 (1)、画出△AOB平移后的三角形,其平移的方向为射线AD的方向,平移的距离为线段AD的长;(2)、观察平移后的图形,除了矩形ABCD外还有哪一种特殊的平行四边形?并给出证明.21. 如图,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)、画出△AOB平移后的三角形,其平移的方向为射线AD的方向,平移的距离为线段AD的长;(2)、观察平移后的图形,除了矩形ABCD外还有哪一种特殊的平行四边形?并给出证明.21. 如图,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.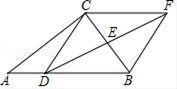 (1)、求证:四边形CDBF是平行四边形;(2)、若∠FDB=30°,∠ABC=45°,BC=4 ,求DF的长.22. “足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
(1)、求证:四边形CDBF是平行四边形;(2)、若∠FDB=30°,∠ABC=45°,BC=4 ,求DF的长.22. “足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)根据所给信息,解答以下问题:
 (1)、在扇形统计图中,C对应的扇形的圆心角是度;(2)、补全条形统计图;(3)、所抽取学生的足球运球测试成绩的中位数会落在等级;(4)、该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?23. 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
(1)、在扇形统计图中,C对应的扇形的圆心角是度;(2)、补全条形统计图;(3)、所抽取学生的足球运球测试成绩的中位数会落在等级;(4)、该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?23. 为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).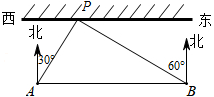 24. 某蔬菜加工公司先后两次收购某时令蔬菜200吨,第一批蔬菜价格为2000元/吨,因蔬菜大量上市,第二批收购时价格变为500元/吨,这两批蔬菜共用去16万元.(1)、求两批次购蔬菜各购进多少吨?(2)、公司收购后对蔬菜进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润800元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
24. 某蔬菜加工公司先后两次收购某时令蔬菜200吨,第一批蔬菜价格为2000元/吨,因蔬菜大量上市,第二批收购时价格变为500元/吨,这两批蔬菜共用去16万元.(1)、求两批次购蔬菜各购进多少吨?(2)、公司收购后对蔬菜进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润800元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?