广西南宁市2018届2018届数学中考二模试卷
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 下列各数中,比-2小的数是( )A、2 B、0 C、-1 D、-32. 如图的几何体是由六个完全相同的正方体组成的,这个几何体的主视图是( )
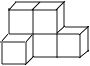 A、
A、 B、
B、 C、
C、 D、
D、 3. 一粒米的质量是 千克,将 用科学记数法表示为A、
3. 一粒米的质量是 千克,将 用科学记数法表示为A、 B、
B、 C、
C、 D、
D、 4. 下列图形中既是中心对称图形又是轴对称图形的是( )。A、
4. 下列图形中既是中心对称图形又是轴对称图形的是( )。A、 B、
B、 C、
C、 D、
D、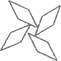 5. 下列各式计算正确的是A、
5. 下列各式计算正确的是A、 B、
B、 C、
C、 D、
D、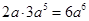 6. 如图, 内接于 ,连接OA,OB,若 ,则 的度数是
6. 如图, 内接于 ,连接OA,OB,若 ,则 的度数是 A、
A、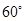 B、
B、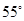 C、
C、 D、
D、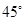 7. 不等式 的正整数解的个数是为A、1 B、2 C、3 D、48. 如图,平行四边形ABCD中,AE平分 , , ,则CE等于
7. 不等式 的正整数解的个数是为A、1 B、2 C、3 D、48. 如图,平行四边形ABCD中,AE平分 , , ,则CE等于 A、6 B、5 C、4 D、39. 某校新生进行军训打靶演练,分小组进行,某小组五名同学的成绩分别是:9、5、8、7、6环,则该组数据的平均数与中位数分别是A、6,7 B、6,8 C、7,7 D、7,810. 如图,图中是抛物线形拱桥,当拱顶离水面2m时水面宽4m.水面下降1m,水面宽度为( )
A、6 B、5 C、4 D、39. 某校新生进行军训打靶演练,分小组进行,某小组五名同学的成绩分别是:9、5、8、7、6环,则该组数据的平均数与中位数分别是A、6,7 B、6,8 C、7,7 D、7,810. 如图,图中是抛物线形拱桥,当拱顶离水面2m时水面宽4m.水面下降1m,水面宽度为( ) A、2 m B、2 m C、 m D、 m11. 如图,半径为4的 与含有 角的直角三角板ABC的边AC切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与 相切时,该直角三角板平移的距离为
A、2 m B、2 m C、 m D、 m11. 如图,半径为4的 与含有 角的直角三角板ABC的边AC切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与 相切时,该直角三角板平移的距离为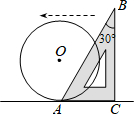 A、2 B、 C、4 D、12. 如图,已知直线 与与双曲线 交于A、B两点,连接OA,若 ,则k的值为
A、2 B、 C、4 D、12. 如图,已知直线 与与双曲线 交于A、B两点,连接OA,若 ,则k的值为 A、 B、
A、 B、 C、
C、 D、
D、
二、填空题
-
13. 一组数据按从小到大的顺序排列为1,2,3,3,4,5,则这组数据的众数是 .14. 如图,已知 , ,垂足为E,若 ,则 的度数为 .
 15. 分解因式: .16. 如图,在菱形ABCD中, , ,则菱形ABCD的周长等于 .
15. 分解因式: .16. 如图,在菱形ABCD中, , ,则菱形ABCD的周长等于 . 17. 如图,下列图形均是由完全相同的点按照一定的规律组成的,第1个图形一共有3个点,第2个图形一共有8个点,第3个图形一共有15个点, ,按此规律排列下去,第100个图形中点的个数是 .
17. 如图,下列图形均是由完全相同的点按照一定的规律组成的,第1个图形一共有3个点,第2个图形一共有8个点,第3个图形一共有15个点, ,按此规律排列下去,第100个图形中点的个数是 . 18. 如图,正方形ABCD边长为6,E是BC的中点,将 沿AE折叠,使点B落在点H处,延长EH交CD于点F,过E作 的平分线交CD于点G,则 的面积为 .
18. 如图,正方形ABCD边长为6,E是BC的中点,将 沿AE折叠,使点B落在点H处,延长EH交CD于点F,过E作 的平分线交CD于点G,则 的面积为 .
三、解答题
-
19. 先化简,再求值: ,其中 .20. 如图,在平面直角坐标系中, , , .
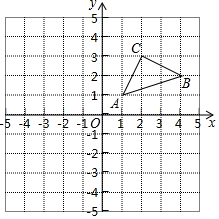 (1)、①清画出将 向下平移3个单位得到的 ;
(1)、①清画出将 向下平移3个单位得到的 ;②请画出以点O为旋转中心,将 逆时针旋转 得到的
(2)、请直接写出 、 的距离.21. 如图,在 中, ,点C为AB的中点, ,以点O为圆心,6为半径的圆经过点C,分别交OA、OB于点E、F. (1)、求证:AB为 的切线;(2)、求图中阴影部分的面积 注:结果保留 , , ,22. 荔枝是广西盛产的一种水果,六月份是荔技传统销售旺季 去年六月份某水果公司为拓展销售渠道,在实体店的基础上中途增设了网店,公司总销售量 吨 与销售时间 天 关系如图所示:
(1)、求证:AB为 的切线;(2)、求图中阴影部分的面积 注:结果保留 , , ,22. 荔枝是广西盛产的一种水果,六月份是荔技传统销售旺季 去年六月份某水果公司为拓展销售渠道,在实体店的基础上中途增设了网店,公司总销售量 吨 与销售时间 天 关系如图所示: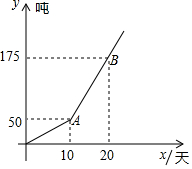 (1)、请直接写出去年六月份网店每天的销售量,并求出AB的解析式 不写取值范围 ;(2)、公司预计,今年六月份实体店的销售量与去年相同,网店的销售量将有所增加,预计今年网店每天的销售量比去年增加 ,公司六月份的总销售量是去年的 倍,求m的值.23. 计算: .24. 某校英语社团举行了“单词听写大赛”,每位参赛选手共听写单词100个 现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:组: ,B组: ,C组: ,D组: ,E组: 并绘制了如下不完整的统计图:
(1)、请直接写出去年六月份网店每天的销售量,并求出AB的解析式 不写取值范围 ;(2)、公司预计,今年六月份实体店的销售量与去年相同,网店的销售量将有所增加,预计今年网店每天的销售量比去年增加 ,公司六月份的总销售量是去年的 倍,求m的值.23. 计算: .24. 某校英语社团举行了“单词听写大赛”,每位参赛选手共听写单词100个 现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:组: ,B组: ,C组: ,D组: ,E组: 并绘制了如下不完整的统计图:
请根据以上信息解答下列问题:
(1)、本次调查共抽取了多少名学生,并将条形统计图补充完整;(2)、求出A组所对的扇形圆心角的度数;(3)、若从D、E两组中分别抽取一位学生进行采访,请用画树状图或列表法求出恰好抽到两位女学生的概率.25. 如图, 和 都是等腰直角三角形, , , 的顶点A在 的斜边DE上,AB、CD交于点F,连接BD. (1)、求证: ≌ ;(2)、求证: ;(3)、若 ,AF: :3,求线段AB的长.26. 如图1,抛物线 经过 , 两点,抛物线与x轴的另一交点为A,连接AC、BC.
(1)、求证: ≌ ;(2)、求证: ;(3)、若 ,AF: :3,求线段AB的长.26. 如图1,抛物线 经过 , 两点,抛物线与x轴的另一交点为A,连接AC、BC.
 (1)、求抛物线的解析式及点A的坐标;(2)、若点D是线段AC的中点,连接BD,在y轴上是否存一点E,使得 是以BD为斜边的直角三角形?若存在,求出点E的坐标,若不存在,说明理由;(3)、如图2,P为抛物线在第一象限内一动点,过P作 于Q,当PQ的长度最大时,在线段BC上找一点M使 的值最小,求 的最小值.
(1)、求抛物线的解析式及点A的坐标;(2)、若点D是线段AC的中点,连接BD,在y轴上是否存一点E,使得 是以BD为斜边的直角三角形?若存在,求出点E的坐标,若不存在,说明理由;(3)、如图2,P为抛物线在第一象限内一动点,过P作 于Q,当PQ的长度最大时,在线段BC上找一点M使 的值最小,求 的最小值.