广西贵港市平南县2018届数学中考一模试卷
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. ﹣3的倒数是( )A、﹣3 B、3 C、 ﹣
 D、
D、
-
2. 一天时间为86400秒,用科学记数法表示这一数据是( )A、864×102 B、86.4×103 C、8.64×104 D、0.864×105
-
3. 若一个等腰三角形的两边长分别为 和 ,则这个等腰三角形的周长是为( ).A、 B、 C、 或 D、
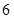 或
或
-
4. 下列命题中,属于真命题的是( )A、平分弦的直径垂直于弦,并且平分弦所对的两条弧 B、同位角相等 C、对角线互相垂直的四边形是菱形 D、 若a=b,则

-
5. 一组数据5、a、4、3、2的平均数是3,则这组数据的方差为( )A、0 B、
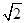 C、2
D、10
C、2
D、10
-
6. 若点M(﹣3,m)、N(﹣4,n)都在反比例函数y= (k≠0)图象上,则m和n的大小关系是( )A、m<n B、m>N C、m=n D、不能确定
-
7. 如图,⊙O的半径为5,弦AB的长为8,点M在线段AB(包括端点A,B)上移动,则OM的取值范围是( )
 A、3≤OM≤5 B、3≤OM<5 C、4≤OM≤5 D、4≤OM<5
A、3≤OM≤5 B、3≤OM<5 C、4≤OM≤5 D、4≤OM<5 -
8. 关于x的一元二次方程x2﹣ax+ =0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定
-
9. 如图,把一块含有30°角的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处,桌面的另一个顶点F与三角板斜边相交于点F,如果∠1=50°,那么∠AFE的度数为( )
 A、10° B、20° C、30° D、40°
A、10° B、20° C、30° D、40° -
10. 在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )A、
 B、
B、 C、
C、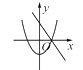 D、
D、
-
11. 如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数至少为( )
 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8
二、填空题
-
12. 计算:2a×(﹣2b)= .
-
13. 分解因式:3a2﹣6a+3= .
-
14. 圆锥底面圆的半径为4cm,其侧面展开图的圆心角120°,则圆锥母线长为cm.
-
15. 将抛物线y=﹣x2+1向右平移2个单位长度,再向上平移3个单位长度所得的抛物线解析式为 .
-
16. 如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .

-
17. 如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1 , 且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2 , 且A2O=2A1O,…,依此规律,得到等腰直角三角形A2018OB2018 , 则点A2018的坐标为 .

三、解答题
-
18.(1)、计算:﹣22+|2sin60°|+( )﹣1+π0;(2)、解方程: =1
-
19. 如图,在直角三角形ABC中,
 (1)、过点A作AB的垂线与∠B的平分线相交于点D
(1)、过点A作AB的垂线与∠B的平分线相交于点D(要求:尺规作图,保留作图痕迹,不写作法);
(2)、若∠A=30°,AB=2,则△ABD的面积为 . -
20. 如图,在平面直角坐标系中,一次函数y=nx+2的图象与反比例函数y= 在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且sin∠AOC= .
 (1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积.(3)、请直接写出nx≤ ﹣2的解集.
(1)、求一次函数和反比例函数的解析式;(2)、求△AOB的面积.(3)、请直接写出nx≤ ﹣2的解集. -
21. 某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级
分值
频数
优秀
90﹣100分
良好
75﹣89分
13
合格
60﹣74分
不合格
0﹣59分
9

根据统计图表给出的信息,解答下列问题:
(1)、九年级(1)班共有多少名学生?(2)、体育成绩为优秀的频数是 , 合格的频数为;(3)、若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 . -
22. 某海尔专卖店春节期间,销售10台Ⅰ型号洗衣机和20台Ⅱ型号洗衣机的利润为4000元,销售20台Ⅰ型号洗衣机和10台Ⅱ型号洗衣机的利润为3500元.(1)、求每台Ⅰ型号洗衣机和Ⅱ型号洗衣机的销售利润;(2)、该商店计划一次购进两种型号的洗衣机共100台,其中Ⅱ型号洗衣机的进货量不超过Ⅰ型号洗衣机的进货量的2倍,问当购进Ⅰ型号洗衣机多少台时,销售这100台洗衣机的利润最大?最大利润是多少?
-
23. 如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.
 (1)、求证:直线DM是⊙O的切线;(2)、若DF=2,且AF=4,求BD和DE的长.
(1)、求证:直线DM是⊙O的切线;(2)、若DF=2,且AF=4,求BD和DE的长. -
24. 如图,已知抛物线y=ax2+bx+3过等腰Rt△BOC的两顶点B、C,且与x轴交于点A(﹣1,0).
 (1)、求抛物线的解析式;(2)、抛物线的对称轴与直线BC相交于点M,点N为x轴上一点,当以M,N,B为顶点的三角形与△ABC相似时,求BN的长度;(3)、P为线段BC上方的抛物线上的一个动点,P到直线BC的距离是否存在最大值?若存在,请求出这个最大值的大小以及此时点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、抛物线的对称轴与直线BC相交于点M,点N为x轴上一点,当以M,N,B为顶点的三角形与△ABC相似时,求BN的长度;(3)、P为线段BC上方的抛物线上的一个动点,P到直线BC的距离是否存在最大值?若存在,请求出这个最大值的大小以及此时点P的坐标;若不存在,请说明理由. -
25. 已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
 (1)、请问EG与CG存在怎样的数量关系,并证明你的结论;(2)、将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
(1)、请问EG与CG存在怎样的数量关系,并证明你的结论;(2)、将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)、将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)
