广西贵港市平南县2018届数学中考模拟试卷(5月份)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 若一个数的倒数是﹣2 ,则这个数是( )A、
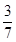 B、 ﹣
B、 ﹣ 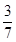 C、
C、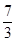 D、 ﹣
D、 ﹣ 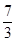 2. 下列运算正确的是( )A、a3﹣a2=a B、a2•a3=a6 C、a6÷a2=a3 D、(a2)3=a63. 下列四个从左到右的变形中,是因式分解是的( )A、(x+1)(x﹣1)=x2﹣1 B、(a+b)(m﹣n)=(m﹣n)(a+b) C、a2﹣8ab+16b2=(a﹣4b)2 D、m2﹣2m﹣3=m(m﹣2)﹣34. 如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点E,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CEP与△DEQ的面积和的变化情况是( )
2. 下列运算正确的是( )A、a3﹣a2=a B、a2•a3=a6 C、a6÷a2=a3 D、(a2)3=a63. 下列四个从左到右的变形中,是因式分解是的( )A、(x+1)(x﹣1)=x2﹣1 B、(a+b)(m﹣n)=(m﹣n)(a+b) C、a2﹣8ab+16b2=(a﹣4b)2 D、m2﹣2m﹣3=m(m﹣2)﹣34. 如图,AB是⊙O的直径,AB=10,P是半径OA上的一动点,PC⊥AB交⊙O于点C,在半径OB上取点Q,使得OQ=CP,DQ⊥AB交⊙O于点D,点C,D位于AB两侧,连接CD交AB于点E,点P从点A出发沿AO向终点O运动,在整个运动过程中,△CEP与△DEQ的面积和的变化情况是( )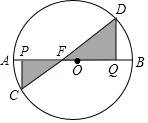 A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大5. 由5个完全相同的小长方形搭成的几何体的主视图和左视图如图所示,则这个几何体的俯视图是( )
A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大5. 由5个完全相同的小长方形搭成的几何体的主视图和左视图如图所示,则这个几何体的俯视图是( ) A、
A、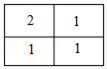 B、
B、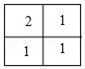 C、
C、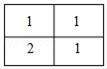 D、
D、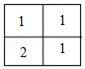 6. 对于抛物线y= (x+4)2﹣5,下列说法正确的是( )A、开口向下 B、对称轴是直线x=4 C、顶点坐标(4,﹣5 ) D、 向右平移4个单位,再向上平移5个单位得到y= x27. 下列命题中正确的个数是( )
6. 对于抛物线y= (x+4)2﹣5,下列说法正确的是( )A、开口向下 B、对称轴是直线x=4 C、顶点坐标(4,﹣5 ) D、 向右平移4个单位,再向上平移5个单位得到y= x27. 下列命题中正确的个数是( )①直角三角形的两条直角边长分别是6和8,那么它的外接圆半径为 ;②如果两个直径为10厘米和6厘米的圆,圆心距为16厘米,那么两圆外切;③过三点可以确定一个圆;④两圆的公共弦垂直平分连心线.
A、0个 B、4个 C、2个 D、3个8. 如图,A、B、C是⊙O上的三点,若∠A+∠C=75°,则∠AOC的度数为( )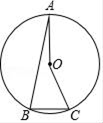 A、150° B、140° C、130° D、120°9. 如图,在平面直角坐标系中,梯形OACB的顶点O是坐标原点,OA边在y轴正半轴上,OB边在x轴正半轴上,且OA∥BC,双曲线y= (x>0)经过AC边的中点,若S梯形OACB=4,则双曲线y= 的k值为( )
A、150° B、140° C、130° D、120°9. 如图,在平面直角坐标系中,梯形OACB的顶点O是坐标原点,OA边在y轴正半轴上,OB边在x轴正半轴上,且OA∥BC,双曲线y= (x>0)经过AC边的中点,若S梯形OACB=4,则双曲线y= 的k值为( )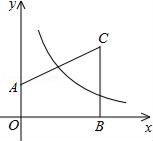 A、5 B、4 C、3 D、210. 如图,点D是正△ABC内的一点,DB=3,DC=4,DA=5,则∠BDC的度数是( )
A、5 B、4 C、3 D、210. 如图,点D是正△ABC内的一点,DB=3,DC=4,DA=5,则∠BDC的度数是( )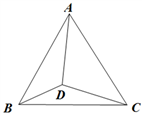 A、120° B、135° C、140° D、150°11.
A、120° B、135° C、140° D、150°11.如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
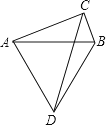 A、75° B、45° C、30° D、15°12. 在矩形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,点P是对角线OC上的任意一点(不包括端点),以P为圆心的圆与AD相切,则⊙P与AB的位置关系是( )A、相离 B、相切 C、相交 D、不确定13. 函数y= 的自变量x的取值范围是 .
A、75° B、45° C、30° D、15°12. 在矩形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,点P是对角线OC上的任意一点(不包括端点),以P为圆心的圆与AD相切,则⊙P与AB的位置关系是( )A、相离 B、相切 C、相交 D、不确定13. 函数y= 的自变量x的取值范围是 .二、填空题
-
14. 计算:﹣2﹣(﹣7)的结果为 .15. 科学家发现,距离地球2540000光年之遥的仙女星系正在向银河系靠近.其中2540000用科学记数法表示为 .16. 已知圆锥的侧面积是40π,底面圆直径为2,则圆锥的母线长是 .17. 二次函数y=ax2+bx+c的图象如图所示,给出下列说法:
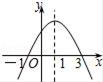
①abc<0;②方程ax2+bx+c=0的根为x1=﹣1、x2=3;③当x>1时,y随x值的增大而减小;④当y>0时,﹣1<x<3.其中正确的说法是( ).
A、①; B、①②; C、①②③; D、①②③④18. 如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y= x于点B1 , 以A1B1为边在A1B1的右侧作等边△A1B1C1 , 再过点C1作A2B2∥y轴,分别交直线x轴和直线y= x于A2 , B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为(用含正整数n的代数式表示).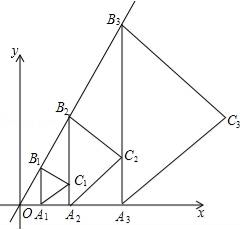
三、解答题
-
19.(1)、计算:(﹣ )﹣1﹣|1- |+2sin60°+(π﹣4)0(2)、解不等式组 .并写出它的整数解.20. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(3,4)、B(1,1)、C(4,2).
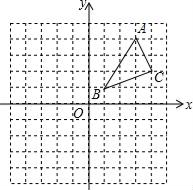 (1)、画出△ABC绕点B逆时针旋转90°后得到的△A1BC1 , 其中A、C分别和A1、C1对应.(2)、平移△ABC,使得A点落在x轴上,B点落在y轴上,画出平移后的△A2B2C2 , 其中A、B、C分别和A2B2C2对应.(3)、填空:在(2)的条件下,设△ABC,△A2B2C2的外接圆的圆心分别为M、M2 , 则MM2= .21. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D,且B(3,﹣1),求:
(1)、画出△ABC绕点B逆时针旋转90°后得到的△A1BC1 , 其中A、C分别和A1、C1对应.(2)、平移△ABC,使得A点落在x轴上,B点落在y轴上,画出平移后的△A2B2C2 , 其中A、B、C分别和A2B2C2对应.(3)、填空:在(2)的条件下,设△ABC,△A2B2C2的外接圆的圆心分别为M、M2 , 则MM2= .21. 如图,已知点A(1,a)是反比例函数y1= 的图象上一点,直线y2=﹣ 与反比例函数y1= 的图象的交点为点B、D,且B(3,﹣1),求: (1)、求反比例函数的解析式;(2)、求点D坐标,并直接写出y1>y2时x的取值范围;(3)、动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.22. “校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题:
(1)、求反比例函数的解析式;(2)、求点D坐标,并直接写出y1>y2时x的取值范围;(3)、动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.22. “校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了两幅尚不完整的统计图,如图所示,请根据统计图中所提供的信息解答下列问题: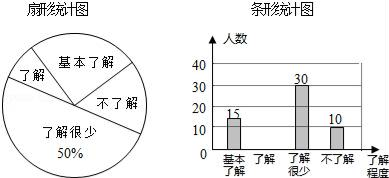 (1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.23. 我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.(1)、求购买A,B两种树苗每棵各需多少元?(2)、考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?(3)、某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?24. 如图,已知Rt△ABC中,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.
(1)、接受问卷调查的学生共有人,扇形统计图中“基本了解”部分所对应扇形的圆心角为;(2)、请补全条形统计图;(3)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.23. 我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.(1)、求购买A,B两种树苗每棵各需多少元?(2)、考虑到绿化效果和资金周转,购进A种树苗不能少于52棵,且用于购买这两种树苗的资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?(3)、某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?24. 如图,已知Rt△ABC中,∠C=90°,D为BC的中点,以AC为直径的⊙O交AB于点E.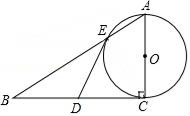 (1)、求证:DE是⊙O的切线;(2)、若AE:EB=1:2,BC=6,求⊙O的半径.25. 抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B( ,0),且与y轴相交于点C.
(1)、求证:DE是⊙O的切线;(2)、若AE:EB=1:2,BC=6,求⊙O的半径.25. 抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B( ,0),且与y轴相交于点C.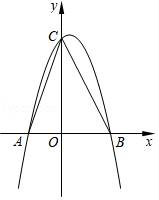 (1)、求这条抛物线的表达式;(2)、求∠ACB的度数;(3)、设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.26. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.
(1)、求这条抛物线的表达式;(2)、求∠ACB的度数;(3)、设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.26. 如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.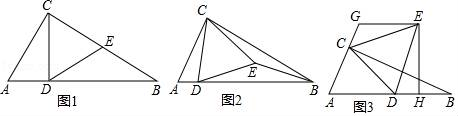 (1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
(1)、如图1,当点E在边BC上时,求证DE=EB;(2)、如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;(3)、如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.