广西北部湾经济区四市同城2018届数学中考模拟试卷(6月份)
试卷更新日期:2019-03-06 类型:中考模拟
一、单选题
-
1. 如图,∠BCD=90°,AB∥DE,则α与β一定满足的等式是( )
 A、α+β=180° B、α+β=90° C、β=3α D、α﹣β=90°2. 把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( )
A、α+β=180° B、α+β=90° C、β=3α D、α﹣β=90°2. 把图中阴影部分的小正方形移动一个,使它与其余四个阴影部分的正方形组成一个既是轴对称又是中心对称的新图形,这样的移法,正确的是( ) A、6→3 B、7→16 C、7→8 D、6→153. 我市今年参加中考人数约为42000人,将42000用科学记数法表示为( )A、4.2×104 B、0.42×105 C、4.2×103 D、42×1034. 下列运算中不正确的是( )A、a3+a2=a5 B、a3•a2=a5 C、a3÷a2=a D、(a3)2=a65. 下列调查中,适宜采用普查方式的是( )A、调查电视台节目的收视率 B、调查市民对皮影表演艺术的喜爱程度 C、调查炮弹的杀伤力的情况 D、调查宇宙飞船的零部件质量6. 在△ABC中,点D,E分别是边AB,BC的中点.若DE=6,则AC=( )A、8 B、10 C、12 D、147. 一个不透明的袋子里装有质地、大小都相同的3个红球和1个绿球;随机从中摸出一球,不再放回,充分搅均后再随机摸出一球。则两次都摸到红球的概率是( )A、 B、 C、 D、8. 若一元二次方程x2+2x+m=0中的b2﹣4ac=0,则这个方程的两根为( )A、x1=1,x2=﹣1 B、x1=x2=1 C、x1=x2=﹣1 D、不确定9. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
A、6→3 B、7→16 C、7→8 D、6→153. 我市今年参加中考人数约为42000人,将42000用科学记数法表示为( )A、4.2×104 B、0.42×105 C、4.2×103 D、42×1034. 下列运算中不正确的是( )A、a3+a2=a5 B、a3•a2=a5 C、a3÷a2=a D、(a3)2=a65. 下列调查中,适宜采用普查方式的是( )A、调查电视台节目的收视率 B、调查市民对皮影表演艺术的喜爱程度 C、调查炮弹的杀伤力的情况 D、调查宇宙飞船的零部件质量6. 在△ABC中,点D,E分别是边AB,BC的中点.若DE=6,则AC=( )A、8 B、10 C、12 D、147. 一个不透明的袋子里装有质地、大小都相同的3个红球和1个绿球;随机从中摸出一球,不再放回,充分搅均后再随机摸出一球。则两次都摸到红球的概率是( )A、 B、 C、 D、8. 若一元二次方程x2+2x+m=0中的b2﹣4ac=0,则这个方程的两根为( )A、x1=1,x2=﹣1 B、x1=x2=1 C、x1=x2=﹣1 D、不确定9. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
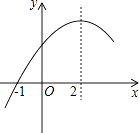 A、1个 B、2个 C、3个 D、4个10. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺.设木长为x尺,绳子长为y尺,则下列符合题意的方程组是( )A、
A、1个 B、2个 C、3个 D、4个10. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺.设木长为x尺,绳子长为y尺,则下列符合题意的方程组是( )A、 B、
B、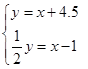 C、
C、 D、
D、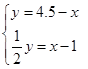 11. 如图,点A,B,C,D,E,F,G,H为⊙O的八等分点,AD与BH的交点为I,若⊙O的半径为1,则HI的长等于( )
11. 如图,点A,B,C,D,E,F,G,H为⊙O的八等分点,AD与BH的交点为I,若⊙O的半径为1,则HI的长等于( ) A、2﹣ B、2+ C、2
A、2﹣ B、2+ C、2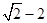 D、
D、 12. 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y= (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( )
12. 如图,将直线y=x向下平移b个单位长度后得到直线l,l与反比例函数y= (k>0,x>0)的图象相交于点A,与x轴相交于点B,则OA2﹣OB2=10,则k的值是( ) A、5 B、10 C、15 D、20
A、5 B、10 C、15 D、20二、填空题
-
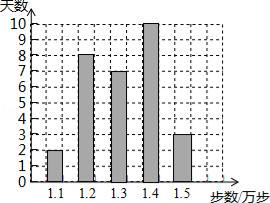
13. 若 有意义,则x的取值范围为 .14. 生命在于运动.运动渗透在生命中的每一个角落,运动的好处就在于让我们的身体保持在健康的状态.小明同学用手机软件记录了11月份每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天所走的步数这组数据中,中位数是万步.
 15. 分解因式(xy﹣1)2﹣(x+y﹣2xy)(2﹣x﹣y)= .16. 如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是 .
15. 分解因式(xy﹣1)2﹣(x+y﹣2xy)(2﹣x﹣y)= .16. 如图,在⊙O中,圆周角∠ACB=150°,弦AB=4,则扇形OAB的面积是 . 17. 如图①,②,③,④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第8个“广”字中的棋子个数是 .
17. 如图①,②,③,④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第8个“广”字中的棋子个数是 . 18. 如图,在平面直角坐标系中,△DEF是由△ABC旋转得到的,则旋转的角度是°.
18. 如图,在平面直角坐标系中,△DEF是由△ABC旋转得到的,则旋转的角度是°.
三、解答题
-
19. 计算:( ﹣1)2+3tan30°﹣( ﹣2)( +2)+2sin60°.20. 解不等式 ,并在数轴上表示不等式组的解.21. 如图,在平行四边形ABCD中,AB<BC.
 (1)、利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)、若BC=7,CD=5,求CE的长.22. 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
(1)、利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)、若BC=7,CD=5,求CE的长.22. 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:分 组
频数
频率
第一组(0≤x<15)
3
0.15
第二组(15≤x<30)
6
a
第三组(30≤x<45)
7
0.35
第四组(45≤x<60)
b
0.20
 (1)、频数分布表中a= , b= , 并将统计图补充完整;(2)、如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)、已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?23. 如图,一艘船在A处望见灯塔E在北偏东60°方向上,此船沿正东方向航行60海里后到达B处,在B处测得灯塔E在北偏东15°方向上.
(1)、频数分布表中a= , b= , 并将统计图补充完整;(2)、如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)、已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?23. 如图,一艘船在A处望见灯塔E在北偏东60°方向上,此船沿正东方向航行60海里后到达B处,在B处测得灯塔E在北偏东15°方向上.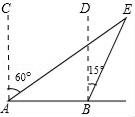
(Ⅰ)求∠AEB的度数;
(Ⅱ)①求A处到灯塔E的距离AE;
②已知灯塔E周围40海里内有暗礁,问:此船继续向东方向航行,有无触礁危险?(参考数据: ≈1.414, ≈1.732)
24. 某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.(1)、求每辆A,B两种自行车的进价分别是多少?(2)、现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.25. 如图,⊙O中,AB是⊙O的直径,G为弦AE的中点,连接OG并延长交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC. (1)、求证:BC是⊙O的切线;(2)、⊙O的半径为5,tanA= ,求FD的长.26. 如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)、求证:BC是⊙O的切线;(2)、⊙O的半径为5,tanA= ,求FD的长.26. 如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D. (1)、求顶点D的坐标(用含a的代数式表示);(2)、若以AD为直径的圆经过点C.
(1)、求顶点D的坐标(用含a的代数式表示);(2)、若以AD为直径的圆经过点C.①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.