湖北省襄阳市襄城区2017-2018学年七年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 在数-(-3),0,(-3)2 , |-9|,-24中,正数的个数有( )A、1个 B、2个 C、3个 D、4个2. 下列说法中错误的是( )A、
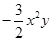 的系数是
的系数是  B、0是单项式
C、
B、0是单项式
C、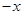 是一次单项式
D、
是一次单项式
D、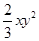 的次数是2
3. 若关于 的方程 的解为 ,则 的值为( )A、-5 B、5 C、-7 D、74. 已知∠A=70°,则∠A的余角等于( )A、20° B、30° C、70° D、110°5. 由四舍五入得到的近似数 ,下列说法正确的是( )A、精确到十分位 B、精确到百位 C、精确到个位 D、精确到千位6. 组成多项式 的单项式是下列几组中的( )A、
的次数是2
3. 若关于 的方程 的解为 ,则 的值为( )A、-5 B、5 C、-7 D、74. 已知∠A=70°,则∠A的余角等于( )A、20° B、30° C、70° D、110°5. 由四舍五入得到的近似数 ,下列说法正确的是( )A、精确到十分位 B、精确到百位 C、精确到个位 D、精确到千位6. 组成多项式 的单项式是下列几组中的( )A、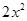 ,x,3
B、
,x,3
B、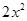 ,-x,-3
C、
,-x,-3
C、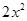 ,x,-3
D、
,x,-3
D、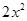 ,-x,3
7. 将一个无盖正方体形状的盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )A、
,-x,3
7. 将一个无盖正方体形状的盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )A、 B、
B、 C、
C、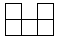 D、
D、 8. 观察图形,下列说法正确的个数是( )
8. 观察图形,下列说法正确的个数是( )( 1 )直线BA和直线AB是同一条直线;(2)AB+BD>AD;(3)射线AC和射线AD是同一条射线;(4)三条直线两两相交时,一定有三个交点
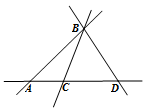 A、1个 B、2个 C、3个 D、4个9. 一个长方形的周长为6a+8b,其中一边的长为2a-b,则另一边的长为( )A、
A、1个 B、2个 C、3个 D、4个9. 一个长方形的周长为6a+8b,其中一边的长为2a-b,则另一边的长为( )A、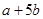 B、
B、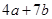 C、
C、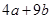 D、
D、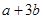 10. 成都市为减少雾霾天气采取了多项措施,如对城区主干道进行绿化.现计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )A、5(x+21﹣1)=6(x﹣1) B、5(x+21)=6(x﹣1) C、5(x+21﹣1)=6x D、5(x+21)=6x11. 如图,将一副三角板叠放在一起,使直角的顶点重合于 ,则 ( )
10. 成都市为减少雾霾天气采取了多项措施,如对城区主干道进行绿化.现计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )A、5(x+21﹣1)=6(x﹣1) B、5(x+21)=6(x﹣1) C、5(x+21﹣1)=6x D、5(x+21)=6x11. 如图,将一副三角板叠放在一起,使直角的顶点重合于 ,则 ( )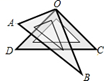 A、
A、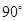 B、
B、 C、
C、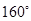 D、
D、
二、填空题
-
12. 中国的领水面积约为370000 ,将370000用科学记数法表示为.13. 若 , ,则 的值为 .14. 用一根长60m的绳子围出一个长方形,使它的长是宽的1.5倍,那么这个长方形的长是m.15. 已知线段AB=12cm,点M是它一个三等分点,则AM=cm.16. 若有理数a,b,c在数轴上的位置如图所示,则化简: .
 17. 如果 和 互补,且 ,则下列式子中:① ;② ;
17. 如果 和 互补,且 ,则下列式子中:① ;② ;③ ;④ ,可以表示 的余角的有(填序号即可).
三、解答题
-
18. 计算:(1)、(2)、(3)、19. 解方程:(1)、(2)、 .20. 已知关于x的方程 的解是 ,求代数式 的值.21. 一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的速度和两城之间的航程.22. 点A、B、C是同一直线上的三点,并且AB=20cm,BC=14cm.若点M是AB中点,点N是BC中点.(1)、求MN的长.23. 马刚家附近有甲乙两家超市,春节来临之际两个超市分别给出了不同的促销方案:甲超市购物全场8.8折,乙超市购物①不超过200元,不给予优惠;②超过200元而不超过500元,打9折;③超过500元,其中的500元仍打9折,超过500元的部分打8折.(假设两家超市相同商品的标价都一样)(1)、当一次性购物标价总额是300元时,甲乙两个超市实付款分别是多少?(2)、当标价总额是多少元时,甲乙超市实付款一样?24. 如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
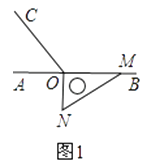 (1)、如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且 OM恰好平分∠BOC.此时∠AOM=度;
(1)、如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且 OM恰好平分∠BOC.此时∠AOM=度;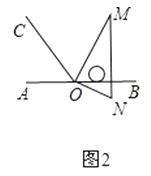 (2)、如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(2)、如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;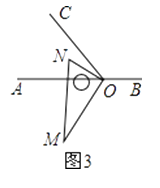 (3)、将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
(3)、将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .