河南省南阳市镇平县2017-2018学年七年级上学期数学期末考试试卷

试卷更新日期：2019-03-06 类型：期末考试

进入出卷网下载

一、单选题

1. －5的绝对值（）

A、5 B、－5 C、 $\frac{1}{5}$ D、

查看试题解析
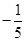2. 关于近似数6.8×10³ ，下列说法中正确的是（）

A、精确到十分位 B、精确到个位 C、精确到百位 D、精确到千位

查看试题解析
3. 若a＜0，则下列各式不正确的是（）

A、a³=（﹣a）³ B、a²=|a²| C、a²=（﹣a）² D、a³=﹣（﹣a³）

查看试题解析
4. 如图，已知直线a、b被直线c所截．若a∥b，∠1=120°，则∠2的度数为（）

A、50° B、60° C、120° D、130°

查看试题解析
5. 一个多项式A与多项式B＝2x²－3xy－y²的和是多项式C＝x²＋xy＋y² ，则A等于（）

A、x²－4xy－2y² B、－x²＋4xy＋2y² C、3x²－2xy－2y² D、3x²－2xy

查看试题解析
6. 如图是正方体的展开图，则原正方体相对两个面上的数字之和的最小值是（）

A、3 B、6 C、7 D、8

查看试题解析
7. 当x=1时， $a x + b + 1$ 的值为−2，则 $(a + b - 1) (1 - a - b)$ 的值为（）

A、− 16 B、− 8 C、8 D、16

查看试题解析
8. 下列四个生活、生产现象：
①用两个钉子就可以把木条固定在墙上；
②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；
③从A地到B地架设电线，总是尽可能沿着线段AB架设；
④把弯曲的公路改直，就能缩短路程，其中可用公理“两点之间，线段最短”来解释的现象有（）

A、①② B、①③ C、②④ D、③④

查看试题解析
9. 以下四个条件中，能得到互相垂直关系的有（）
①对顶角的平分线；②平行线截得的一组同旁内角的平分线；③平行线截得的一组同位角的平分线；④平行线截得的一组内错角的平分线．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10.
观察图中正方形四个顶点所标的数字规律，可知，数2016应标在（）

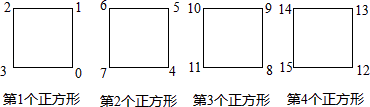A、第504个正方形的左下角 B、第504个正方形的右下角 C、第505个正方形的左上角 D、第505个正方形的右下角

查看试题解析

二、填空题

11. 计算：3a²﹣a²= ．

查看试题解析
12.
如图，由五个小正方体组成的几何体中，若每个小正方体的棱长都是1，则该几何体的主视图和左视图的面积之和是

查看试题解析
13. 直线AB、CD、EF交于点O，则∠1+∠2+∠3=度．

查看试题解析
14. 在数轴上，点A表示数﹣2，点B到点A的距离为3，则点B表示的数是．

查看试题解析
15. 若把面值为1元的纸币换成面值为1角或5角的硬币，则共有种换法．

查看试题解析

三、解答题

16. 计算：

(1)、 $- 4^{3} \div {(- 2)}^{2} \times \frac{1}{5}$

(2)、 $- (1 - 0.5) \div \frac{1}{3} \times [2 + {(- 4)}^{2}]$ ．

查看试题解析
17. 如图，O是直线AB上一点，OD平分∠AOC．

(1)、若∠AOC=60°，请求出∠AOD和∠BOC的度数.

(2)、若∠AOD和∠DOE互余，且∠AOD= $\frac{1}{3}$ ∠AOE，请求出∠AOD和∠COE的度数．

查看试题解析
18. 先化简，再求值：2xy－ $\frac{1}{2}$ (4xy－8x²y²)＋2(3xy－5x²y²)，其中x＝ $\frac{1}{3}$ ，y＝－3.

查看试题解析
19. 如图是几个小立方块所搭几何体的俯视图，小正方形的数字表示该位置小立方块的个数，请画出这个几何体的主视图和左视图．

查看试题解析
20. 如图，已知AB∥CD，∠B=40°，CN是∠BCE的平分线CM⊥CN．

(1)、求∠BCE的度数；

(2)、求∠BCM的度数．

查看试题解析
21. 某超市在春节期间对顾客实行优惠，规定如下：
一次性购物
优惠办法
少于200元
不予优惠
低于500元但不低于200元
九折优惠
500元或超过500元
其中500元部分给予九折优惠，超过500元部分给予八折优惠

(1)、王老师一次性购物600元，他实际付款元．

(2)、若顾客在该超市一次性购物x元，当x小于500元但不小于200时，他实际付款元，当x大于或等于500元时，他实际付款元．（用含x的代数式表示）．

(3)、如果王老师两次购物货款合计820元，第一次购物的货款为a元（200＜a＜300），用含a的代数式表示：两次购物王老师实际付款多少元？

查看试题解析
22. 如图，已知∠1=∠2，∠3=∠4，∠5=∠A，试说明：BE∥CF．
完善下面的解答过程，并填写理由或数学式：

解：

∵∠3=∠4（已知）

∴AE∥ （          ）

∴∠EDC=∠5（        ）

∵∠5=∠A（已知）

∴∠EDC= （         ）

∴DC∥AB（    ）

∴∠5+∠ABC=180°（        ）

即∠5+∠2+∠3=180°

∵∠1=∠2（已知）

∴∠5+∠1+∠3=180°（        ）

即∠BCF+∠3=180°

∴BE∥CF（      ）．

查看试题解析
23. 如图，已知A，B分别为数轴上的两点，点A表示的数是﹣30，点B表示的数是50．

(1)、请写出线段AB中点M表示的数是．

(2)、现有一只蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左移动，同时另一只蚂蚁Q恰好从点A出发，以每秒2个单位长度的速度沿数轴向右移动，设两只蚂蚁在数轴上的点C相遇．
①求A、B两点间的距离；

②求两只蚂蚁在数轴上的点C相遇时所用的时间；

③求点C对应的数是多少？

(3)、若蚂蚁P从点B出发，以每秒3个单位长度的速度沿数轴向左运动，同时另一只蚂蚁恰好从A点出发，以每秒2个单位长度的速度沿数轴也向左运动，设两只蚂蚁在数轴上的D点相遇，求D点表示的数是多少？

查看试题解析

一次性购物	优惠办法
少于200元	不予优惠
低于500元但不低于200元	九折优惠
500元或超过500元	其中500元部分给予九折优惠，超过500元部分给予八折优惠