浙教版2019中考数学模拟试卷4
试卷更新日期：2019-03-06 类型：中考模拟
一、选择题
-
1. ﹣ 的倒数是（ ）A、
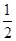B、﹣2
C、2
D、﹣
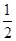2. 若一个三角形三个内角度数的比为2：7：4，那么这个三角形是（ ）A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形3. 在下列调查中，最适宜采用普查方式的是（ ）A、了解我市正在销售的酸奶质量情况 B、了解某校初三年级学生期末立定跳远成绩 C、了解全市中学生对雄安新区的关注程度 D、对全市小学生使用手机玩游戏的情况调查4. 下列计算正确的是（ ）A、a4+a4＝a8 B、3（a﹣2b）＝3a﹣2b C、a5÷a3＝a2 D、（2a﹣b）2＝4a2﹣b25. 如图，在平行四边形ABCD中，AE平分∠DAB，∠AED＝26°，则∠C的度数为（ ）
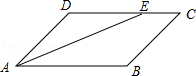A、26° B、42° C、52° D、56°6. 如图，E为▱ABCD的边BC延长线上一点，AE与BD交于点F，与DC交于点G．若BC＝2CE，则AF：FG的值是（ ）
A、3：2 B、2：3 C、5：3 D、4：37. 用配方法解一元二次方程x2+4x﹣3=0时，原方程可变形为（ ）A、（x+2）2=1 B、（x+2）2=7 C、（x+2）2=13 D、（x+2）2=198. 分别写有0，2﹣1 ， ﹣2，cos30°，3的五张卡片，除数不同外其他均相同，从中任意抽取一张，那么抽到负数的概率是（ ）A、
B、
C、
D、
9. 九年级学生去距学校10km的博物馆参观，一部分学生骑自行车先走，过了20min后，其余学生乘汽车出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度．设骑车学生的速度为xkm/h，则所列方程正确的是（ ）A、
＝ 
﹣ 
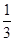B、 ＝ ﹣20
C、 ＝ +
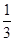D、 ＝ +20
10. 甲、乙两名运动员进行射击练习，每人射击5次，成绩（单位：环）如下表所示：下列说法错误的是（ ）第1次
第2次
第3次
第4次
第5次
平均成绩
甲
7
▲
8
10
8
8
乙
7
8
8
9
8
▲
A、甲运动员的第2次射击成绩为7环 B、乙运动员的平均射击成绩为8环 C、甲运动员这5次射击成绩的方差为6 D、乙运动员的成绩更稳定11. 已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①抛物线的对称轴为x＝﹣1；②abc＝0；③方程ax2+bx+c+1＝0有两个不相等的实数根；④无论x取何值，ax2+bx≤a﹣b．其中，正确的个数为（ ）
A、4 B、3 C、2 D、112. 如图，已知边长为4的正方形ABCD，E是BC边上一动点（与B，C不重合），连结AE，作EF⊥AE交正方形的外角∠DCG的平分线于点F，设BE＝x，△ECF的面积为y，下列图象中，能大致表示y与x的函数关系的是（ ）
A、
B、
C、
D、
二、填空题
-
13. 最近，被称为“史上最大尺度反腐剧”的《人民的名义》引发全民追剧热潮，据统计某周日该剧平台单天播放量超过了惊人的45亿，请将数据45亿用科学记数法表示为 ．14. 若a+b＝2，a﹣b＝﹣3，则a2﹣b2＝ ．15. 分式方程 +1= 的解是 ．16. 分解因式：﹣2x3+4x2y﹣2xy2＝ ．17. 如图，△AOB，AB∥x轴，OB＝2，点B在反比例函数y＝ 上，将△AOB绕点B逆时针旋转，当点O的对应点O′落在x轴的正半轴上时，AB的对应边A′B恰好经过点O，则k的值为 ．
18. 如图，MN为⊙O的直径，四边形ABCD，CEFG均为正方形，若OM＝2 ，则EF的长为 ．
三、解答题
-
19. 解方程组： ．20. 有甲、乙、丙三种糖果混合而成的什锦糖100千克，其中各种糖果的单价和数量如下表所示，商家用加权平均数来确定什锦糖的单价．
甲种糖果
乙种糖果
丙种糖果
单价（元/千克）
15
20
25
千克（千克）
30
40
30
(1)、该什锦糖的单价为元/千克．(2)、为了使什锦糖的单价每千克至少降低2元，商家计划在什锦糖中再加入甲、乙两种糖果共100千克，则最少需要加入甲种糖果多少千克？21. 先化简， ÷（ ﹣ ），再从﹣2＜x＜3中选一个合适的整数代入求值．22. 为推广阳光体育“大课间”活动，我市某中学决定在学生中开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
(1)、在这项调查中，共调查了多少名学生？(2)、请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
(3)、若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到同性别学生的概率．23. 如图，某天上午，一渔船在我海上指挥中心P的南偏东15°方向的B处遇险，在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援，此时，海口舰与指挥中心P相距10（ +1）海里，渔船B在海口舰A的正东方向．求此时渔船B与海口舰A的距离（结果保留根号）．
24. 如图，在正方形ABCD中，动点P在射线CB上（与B、C不重合），连结AP，过D作DF∥AP交直线BC于点F，过F作FE⊥直线BD于点E，连结AE、PE．
(1)、如图1，当点P在线段CB上时①求证：△ABP≌△DCF；
②点P在运动过程中，探究：△AEP的形状是否发生变化，若不变，请判断△AEP的形状，并说明理由；
(2)、如图2，当点P在CB的延长线上时①（1）中的结论②是否成立？不必说明理由；
②若正方形ABCD的边长为1，设BP＝x，当x为何值时，DF平分∠BDC？
25. 如图，在平面直角坐标系中，抛物线y＝mx2﹣8mx+4m+2（m＞0）与y轴交于点A（0，3），与x轴交于点B、C（B在C的左边），直线AD∥x轴交抛物线于点D，x轴上有一动点E（t，0），过点E作平行于y轴的直线l与抛物线、AD分别交于P、Q．
(1)、求抛物线的解析式，并直接写出点B、C的坐标；(2)、当0＜t≤8时，求△APC面积的最大值；(3)、当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．