浙教版2019中考数学模拟试卷2
试卷更新日期：2019-03-06 类型：中考模拟
一、选择题
-
1. 计算 的结果是（ ）A、2 B、±2 C、﹣2 D、42. 若分式 有意义，则x的取值范围是（ ）A、x≠1 B、x＝1 C、x＞1 D、x＜13. 估算 -3的值在（ ）A、1与2之间 B、2与3之间 C、3与4之间 D、5与6之间4. 不等式组 的解集是（ ）A、x≥2 B、﹣1＜x≤2 C、x≤2 D、﹣1＜x≤15. 二次函数y＝（x﹣m）2﹣m2﹣1有最小值﹣4，则实数m的值可能是（ ）A、﹣ B、﹣3 C、 D、46. 如图，在△ABC与△A′B′C中，AB＝AC＝A′B′＝A′C，∠B+∠B′＝90°，△ABC，△A′B′C′的面积分别为S1、S2 ， 则（ ）
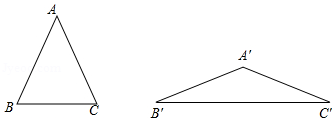A、S1＞S2 B、S1＝S2 C、S1＜S2 D、无法比较S1、S2的大小关系7. 下列语句中，其中正确的个数是（ ）①将多项式a（x﹣y）2﹣b（y﹣x）因式分解，则原式＝（x﹣y）（ax﹣ay+b）；②将多项式x2+4y2﹣4xy因式分解，则原式＝（x﹣2y）2；③90°的圆周角所对的弦是直径；④半圆（或直径）所对的圆周角是直角．
A、1 B、2 C、3 D、48. 如图，已知点A（1，0），B（0，2），以AB为边在第一象限内作正方形ABCD，直线CD与y轴交于点G，再以DG为边在第一象限内作正方形DEFG，若反比例函数y＝ 的图象经过点E，则k的值是（ ）
A、33 B、34 C、35 D、369. 如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB＝30°，点E，F分别是AC，BC的中点，直线EF与⊙O交于G，H两点，若⊙O的半径为6，则GE+FH的最大值为（ ）
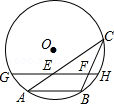A、6 B、9 C、10 D、12二、填空题
-
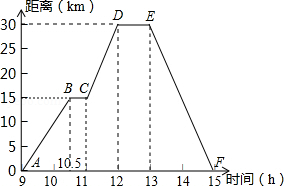
10. 使代数式 有意义的x的取值范围是 ．11. 体育中考前夕，某校将九年级部分男生分成五组，进行了跳绳模拟测试，经统计，这五个小组平均每分钟跳绳次数如下：180，190，x，176，180．若该组数据的众数与平均数相等，那么这组数据的中位数是 ．12. 小强骑自行车去郊游，9时出发，15时返回．如图表示他距家的距离y（千米）与相应的时刻x（时）之间的函数关系的图象．根据这个图象，写出一个正确的结论 ．
13. 已知正实数a，满足a﹣ ＝ ，则a+ ＝ ．14. 如图，把两个等腰直角三角板如图放置，点F为BC中点，AG＝1，BG＝2，则CH的长为 ．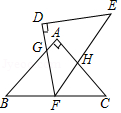
15. 如图，在四边形ABCD中，∠A＝90°，AD＝2，AB﹣BC＝1，圆心在线段BD上的⊙O交AB于点E、F，交BC于点G，H，其EF＝GH，则CD的长为 ．
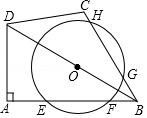16. 抛物线y＝ax2+bx+c的顶点为D（﹣1，2），与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，其部分图象如图，则以下结论：①b2﹣4ac＜0；②当x＞﹣1时y随x增大而减小；③a+b+c＜0；④若方程ax2+bx+c﹣m＝0没有实数根，则m＞2； ⑤3a+c＜0．其中，正确结论的序号是 ．
17. 如图，在△OAB中，AO＝AB，S△AOB＝10，函数y＝ （x＞0）图象与OA交于点C，点D是函数y＝ （x＞0）的图象上一点，且CD∥x轴，若∠ADC＝90°，则k的值是 ．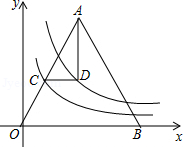
三、解答题
-
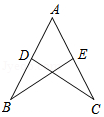
18. 解方程：5x+3＝2（x+3）19. 如图，点D在AB上，点E在AC上，AB＝AC，BD＝CE，求证：∠B＝∠C．
20. 如图，四边形ABCD是平行四边形，E、F是对角线BD上的两点，∠1＝∠2．
(1)、求证：DE＝BF；(2)、求证：四边形AECF是平行四边形．21. 如图，我国某艘海舰船沿正东方向由A向B例行巡航南海部分区域，在航线AB同一水平面上，有三座岛屿C、D、E．船在A处时，测得岛C在A处南偏东15°方向距离A处 a（a＞0）海里，岛D在A处南偏东60°方向距离A处a海里，岛E在A处东南方向，当船航行到达B处时，此时测得岛E恰好在船的正南方．
(1)、请说明船航行的距离AB正好是岛E离开B处的距离；(2)、若岛D距离B处18海里，求岛C、E之间的距离．22. 某数学兴趣小组在全校范围内随机抽取了一些同学进行“我最喜爱的余姚传统小吃”调查活动，将调查问卷整理后绘制成如下两幅不完整的统计图．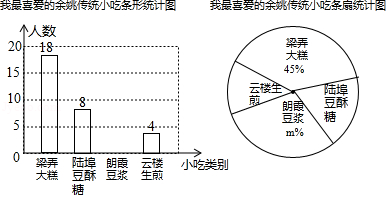
请根据图中的信息，解答下列问题：
(1)、在这次调查中，一共抽取了名学生，m＝ ．(2)、请补全条形统计图；(3)、在扇形统计图中，“陆埠豆酥糖”对应的圆心角为度；(4)、若该校共有1000名学生，请你估计该校学生中最喜爱“云楼生煎”的学生有多少人？23. 阅读下列材料：延庆是全市唯一一个全境域都是水源保护地的区域，森林覆盖率达到57.46%，“干净指数”连续五年全市第一，人均公共绿地面积41.88平方米，空气质量长期保持全市前列．根据区环保局的空气质量的通报，2012年空气质量为优，成为北京市最宜居的地方．
由于经济发展，私家车剧增等原因，2013年空气质量下降为良，尤其是PM2.5平均浓度有所增长，2013年PM2.5平均浓度约为78微克/立方米，比2012年PM2.5平均浓度增长了12.2%．延庆区作为2019年世园会和2022年冬奥会比赛的举办地，将全面治理“煤、气、尘”，逐渐降低PM2.5浓度，力争到2020年降至46微克/立方米，实现“延庆蓝”．
据悉，延庆将大力推广地源热泵、风能、太阳能等新能源和可再生能源．同时强化大货车监管，提升新能源车辆利用率.2020年新能源和可再生能源在延庆的使用比例将达到40%，煤炭能源消费总量占比3%以下，基本建成“无煤区”．
经过全面治理，2014年PM2.5平均浓度约为70微克/立方米，比2013年平均浓度降低了10.26%；2015年PM2.5平均浓度比2014年平均浓度降低了10%，为全市最低；2016年PM2.5平均浓度约为56微克/立方米．
根据以上材料解答下列问题：
(1)、2015年PM2.5平均浓度约为微克/立方米；(2)、选择统计表或统计图，将2013﹣2016年PM2.5平均浓度整理出来；(3)、根据上述材料和绘制的统计表或统计图中提供的信息，预估2017年的PM2.5平均浓度约为微克/立方米；你的预估理由是 ．24. 在平面直角坐标系中，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．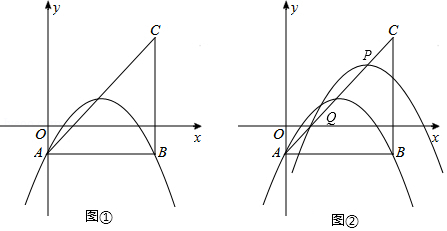
(1)、如图①，若抛物线y＝﹣ x2+bx+c过A、B两点，求该抛物线的函数表达式．(2)、平移（1）中的抛物线，使其顶点在直线AC上滑动（对应的顶点记作点P），且与AC交于另一点Q．①如图②，当点Q在x轴上时，求点P坐标．
②若点M在直线AC下方，且△MPQ是等腰直角三角形，当点M在（1）中所求的抛物线上时，求所有符合条件的点P的坐标．
③取BC的中点N，连接NP、BQ，直接写出NP+BQ的最小值．