新疆乌鲁木齐市2019届九年级上学期数学期末模拟试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形,但不是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 将二次函数y=﹣2x2+6x﹣4配成顶点式为( )A、
A、1个 B、2个 C、3个 D、4个2. 将二次函数y=﹣2x2+6x﹣4配成顶点式为( )A、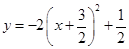 B、
B、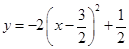 C、
C、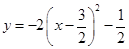 D、
D、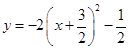 3. 根据你对下列诗词的理解,请你从概率统计的角度判断:所给诗词描述的事件属于随机事件的是( )A、锄禾日当午,汗滴禾下土 B、白日依山尽,黄河入海流 C、离离原上草,一岁一枯荣 D、春眠不觉晓,处处闻啼鸟4. 如图, 是⊙ 的直径,点 , 在⊙ 上.若 ,则 的度数为( )
3. 根据你对下列诗词的理解,请你从概率统计的角度判断:所给诗词描述的事件属于随机事件的是( )A、锄禾日当午,汗滴禾下土 B、白日依山尽,黄河入海流 C、离离原上草,一岁一枯荣 D、春眠不觉晓,处处闻啼鸟4. 如图, 是⊙ 的直径,点 , 在⊙ 上.若 ,则 的度数为( )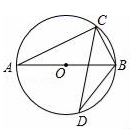 A、 B、 C、 D、5. 已知关于x的一元二次方程mx2+2x-1=0有两个不相等的实数根,则m的取值范围是( )A、m<-1 B、m>1 C、m<1且m≠0 D、m>-1且m≠06. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm7. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、 D、8. 已知函数y=﹣(x﹣m)(x﹣n)+3,并且a,b是方程(x﹣m)(x﹣n)=3的两个根,则实数m,n,a,b的大小关系可能是( )A、m<a<b<n B、m<a<n<b C、a<m<b<n D、a<m<n<b9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
A、 B、 C、 D、5. 已知关于x的一元二次方程mx2+2x-1=0有两个不相等的实数根,则m的取值范围是( )A、m<-1 B、m>1 C、m<1且m≠0 D、m>-1且m≠06. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、2 cm B、4 cm C、2 cm或4 cm D、2 cm或4 cm7. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、 D、8. 已知函数y=﹣(x﹣m)(x﹣n)+3,并且a,b是方程(x﹣m)(x﹣n)=3的两个根,则实数m,n,a,b的大小关系可能是( )A、m<a<b<n B、m<a<n<b C、a<m<b<n D、a<m<n<b9. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )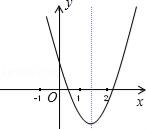 A、1个 B、2个 C、3个 D、4个10. 宾馆有50间房供游客居住,当毎间房每天定价为180元时,宾馆会住满;当毎间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )A、(180+x﹣20)(50﹣
A、1个 B、2个 C、3个 D、4个10. 宾馆有50间房供游客居住,当毎间房每天定价为180元时,宾馆会住满;当毎间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的毎间房每天支出20元的费用.当房价定为多少元时,宾馆当天的利润为10890元?设房价定为x元.则有( )A、(180+x﹣20)(50﹣ )=10890
B、(x﹣20)(50﹣
)=10890
B、(x﹣20)(50﹣ 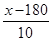 )=10890
C、x(50﹣
)=10890
C、x(50﹣ 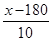 )﹣50×20=10890
D、(x+180)(50﹣
)﹣50×20=10890
D、(x+180)(50﹣  )﹣50×20=10890
)﹣50×20=10890
二、解答题
-
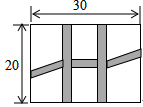
11. 解方程:(x+1)(x+2)=2x+4.12. 如图所示,在长为32m、宽20m的矩形耕地上,修筑同样宽的三条道路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块作试验田,要使试验田面积为570m2 , 问道路应多宽?
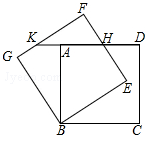
 13. 将一块含30°角的直角三角板OAB和一块等腰直角三角板ODC按如图的方式放置在平面直角坐标系中.已知C、B两点分别在x轴和y轴上,∠ABO=∠D=90°,OB=OC,AB=3.
13. 将一块含30°角的直角三角板OAB和一块等腰直角三角板ODC按如图的方式放置在平面直角坐标系中.已知C、B两点分别在x轴和y轴上,∠ABO=∠D=90°,OB=OC,AB=3.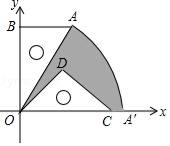 (1)、求边OC的长.(2)、将直角三角板OAB绕点顺时针方向旋转,使OA落在x轴上的OA′位置,求图中阴影部分的面积.14. 某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
(1)、求边OC的长.(2)、将直角三角板OAB绕点顺时针方向旋转,使OA落在x轴上的OA′位置,求图中阴影部分的面积.14. 某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.球
两红
一红一白
两白
礼金券(元)
18
24
18
(1)、请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.(2)、如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.15. 如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.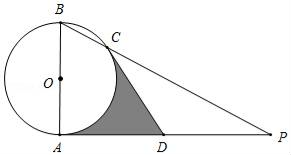 (1)、求证:CD是⊙O的切线;(2)、若AB=2,∠P=30°,求阴影部分的面积.16. 某市城区新建了一“中央商场”,该商场的第4层共分隔成了27间商铺对外招租.据预测:当每间的年租金定为8万元时,可全部租出;每间的年租金每增加0.5万元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺改作其他服务(休闲)用途,每间每年需费用5 000元.(1)、当每间商铺的年租金定为10万元时,能租出间;(2)、当该商场第4层每间商铺的年租金定为多少万元时,该层的年收益(收益=租金-各种费用)为199万元?(3)、当每间商铺的年租金定为万元时, 该“中央商场”的第4层年收益最大,最大收益为 .17. 已知二次函数 的图象过点 (3,0)、 (-1,0).
(1)、求证:CD是⊙O的切线;(2)、若AB=2,∠P=30°,求阴影部分的面积.16. 某市城区新建了一“中央商场”,该商场的第4层共分隔成了27间商铺对外招租.据预测:当每间的年租金定为8万元时,可全部租出;每间的年租金每增加0.5万元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺改作其他服务(休闲)用途,每间每年需费用5 000元.(1)、当每间商铺的年租金定为10万元时,能租出间;(2)、当该商场第4层每间商铺的年租金定为多少万元时,该层的年收益(收益=租金-各种费用)为199万元?(3)、当每间商铺的年租金定为万元时, 该“中央商场”的第4层年收益最大,最大收益为 .17. 已知二次函数 的图象过点 (3,0)、 (-1,0).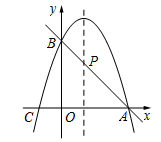 (1)、求二次函数的解析式;(2)、如图,二次函数的图象与 轴交于点 ,二次函数图象的对称轴与直线 交于点 ,求 点的坐标;(3)、在第一象限内的抛物线上有一点 ,当 的面积最大时,求点 的坐标.
(1)、求二次函数的解析式;(2)、如图,二次函数的图象与 轴交于点 ,二次函数图象的对称轴与直线 交于点 ,求 点的坐标;(3)、在第一象限内的抛物线上有一点 ,当 的面积最大时,求点 的坐标.三、填空题
-
18. 在平面直角坐标系中,点A的坐标为(a,3),点B的坐标是(4,b),若点A与点B关于原点O对称,则ab= .19. 一元二次方程x2﹣4x+2=0的两根为x1 , x2 , 则x12﹣4x1+2x1x2的值为 .20. 已知圆锥的底面半径为5cm,侧面积为65πcm2 , 圆锥的母线是 cm.