江苏省苏州市昆山、太仓市2018届九年级上学期数学期末考试试卷

试卷更新日期：2019-03-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程为一元二次方程的是（）

A、x²﹣3＝x(x+4) B、 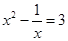C、x²﹣10x＝5 D、4x+6xy＝33

查看试题解析
2. 一元二次方程 x(x﹣2)＝2﹣x 的根是（）

A、﹣1 B、﹣1 和 2 C、1 和 2 D、2

查看试题解析
3. 如图，在 Rt△ABC 中，∠C＝90°，∠B＝30°，AB＝8，则 BC 的长是（）

A、 B、4 $\sqrt{3}$ C、8 $\sqrt{3}$ D、4

查看试题解析
4. 下表是某校女子排球队队员的年龄分布

年龄/岁

13

14

15

16

频数

1

1

7

3

则该校女子排球队队员的平均年龄是（）岁

A、14.5 B、15 C、15.3 D、15.5

查看试题解析
5. 对于二次函数 y＝﹣ $\frac{1}{4}$ x²+x﹣4，下列说法正确的是（）

A、.当 x＞0 时，y 随 x 的增大而增大 B、图象的顶点坐标为(﹣2，﹣7) C、当 x＝2 时，y 有最大值﹣3 D、图象与 x 轴有两个交点

查看试题解析
6. 三角形两边的长分别是 8 和 6，第三边的长是方程 x²﹣12x+20＝0 的一个实数根，则三角形的外接圆半径是（）

A、4 B、5 C、6 D、8

查看试题解析
7. 如图，⊙O是△ABC的外接圆，∠B=60°，⊙O的半径为4，则AC的长等于（）

A、4 $\sqrt{3}$ B、6 $\sqrt{3}$ C、2 $\sqrt{3}$ D、8

查看试题解析
8. 如图，在等腰 Rt△ABC 中，∠C＝90°，AC＝6，D 是 AC 上一点，若 tan∠DBA＝ $\frac{1}{5}$ ，则 AD 的长为（）

A、2 B、 $\sqrt{3}$ C、 D、1

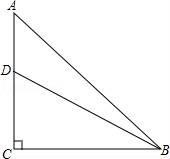查看试题解析
9. 如图，已知△ABC，AB＝BC，以 AB 为直径的圆交 AC 于点 D，过点 D 的⊙O的切线交 BC 于点 E．若 CD＝5，CE＝4，则⊙O 的半径是（）

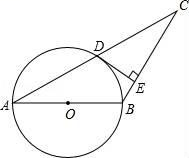A、2 B、4 C、 D、

查看试题解析
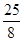10. 如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足 $\frac{C F}{F D} = \frac{1}{3}$ ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED； ②FG=2；③tan∠E= $\frac{\sqrt{5}}{2}$ ； ④S_△_DEF=4 $\sqrt{5}$ ，其中正确的是（）

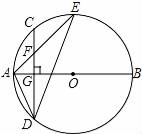A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题

11. 二次函数 y＝x²﹣4x﹣3 的最小值是．

查看试题解析
12. 在一次射击训练中，甲、乙两人各射击 10 次，两人 10 次射击成绩的平均数均是 8.9 环，方差分别是 S _甲²＝1.7，S _乙 ²=1.2，则关于甲、乙两人在这次射击训练中成绩稳定是． (填“甲”或“乙”)

查看试题解析
13. 已知扇形的圆心角为120°，弧长为6π，则扇形的面积是．

查看试题解析
14. 如图所示的六边形广场由若干个大小完全相同的黑色和白色正三角形组成，一只小鸟在广场上随机停留，刚好落在黑色三角形区域的概率为．

查看试题解析
15. 正六边形的外接圆的半径为 4，则这个正六边形的面积为．

查看试题解析
16. 如图，在△ABC 中，AB＝AC＝5，BC＝8．若∠BPC＝ $\frac{1}{2}$ ∠BAC，则 sin∠BPC= .

查看试题解析
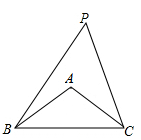
17. 若关于 x 的一元二次方程 x²﹣(k+3)x+2k+2＝0 有一根小于 1，一根大于1，则 k 的取值范围是．

查看试题解析
18. 如图，AB＝6，O是AB的中点，直线l经过点O，∠1＝120°，P是直线l上一点。当△APB为直角三角形时，AP＝．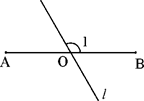

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{4}$ +|sin60°﹣1|+tan45°；

(2)、tan²60°+4sin30°cos45°.

查看试题解析
20. 解方程： $\frac{x}{x - 3} + \frac{x - 3}{x} = \frac{5}{2}$ .

查看试题解析
21. 已知关于 x 的一元二次方程 x²﹣2(k﹣1)x+k(k+2)＝0 有两个不相等的实数根．

(1)、求 k 的取值范围；

(2)、写出一个满足条件的 k 的值，并求此时方程的根．

查看试题解析
22. 在一只不透明的布袋中装有红球 3 个、黄球 1 个，这些球除颜色外都相同，均匀摇匀．

(1)、从布袋中一次摸出 1 个球，计算“摸出的球恰是黄球”的概率；

(2)、从布袋中一次摸出 2 个球，计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程)．

查看试题解析
23. 如图，圆 O 的半径为 1，过点 A(2，0)的直线与圆 O 相切于点 B，与 y 轴相交于点 C．

(1)、求 AB 的长；

(2)、求直线 AB 的解析式．

查看试题解析
24. 如图在塔底的水平面上某点 A 测得塔顶 P 的仰角为α，由此点向塔沿直线行走 m(单位米)到达点 B，测得塔顶的仰角为β，求塔高 PQ 的长．(用 α、β、m 表示)

查看试题解析
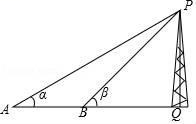25. 如图，锐角△ABC 中 BC＝a，AC＝b，AB＝c，记三角形 ABC 的面积为 S．

(1)、求证：S＝ $\frac{1}{2}$ absinC；

(2)、求证： $\frac{a}{sin A} = \frac{b}{sin B} = \frac{c}{sin C}$ .

查看试题解析
26. 某专卖店经市场调查得知，一种商品的月销售量 Q(单位：吨)与销售价格 x(单位：万元/吨)的关系可用下图中的折线表示．

(1)、写出月销售量 Q 关于销售价格 x 的关系；

(2)、如果该商品的进价为 5 万元/吨，除去进货成本外，专卖店销售该商品每月的固定成本为 10 万元，问该商品每吨定价多少万元时，销售该商品的月利润最大？并求月利润的最大值．

查看试题解析
27. 如图，二次函数 y＝ax²﹣2ax+c(a＞0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点，与 y 轴交于点 C，它的顶点为 P，直线 CP 与过点B 且垂直于 x 轴的直线交于点 D，且 CP：PD＝1：2，tan∠PDB＝ $\frac{4}{3}$ ．

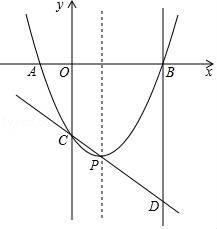(1)、则 A、B 两点的坐标分别为 A( ， )； B( ， )；

(2)、求这个二次函数的解析式；

(3)、在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大，则点M 的坐标为．

查看试题解析
28. 如图，在 Rt△ABC 中，∠ACB＝90°，AC＝6cm，∠ABC＝30°，动点 P 从点 B 出发，在 BA 边上以每秒 2cm 的速度向点 A 匀速运动，同时动点 Q 从点 C 出发，在 CB 边上以每秒 $\sqrt{3}$ cm 的速度向点 B 匀速运动，运动时间为 t 秒(0≤t≤6)，连接 PQ，以 PQ 为直径作⊙O．

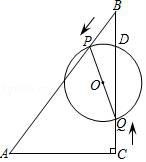(1)、当 t＝1 时，求△BPQ 的面积；

(2)、设⊙O 的面积为 y，求 y 与 t 的函数解析式；

(3)、若⊙O 与 Rt△ABC 的一条边相切，求 t 的值．

查看试题解析

年龄/岁	13	14	15	16
频数	1	1	7	3