河南省郑州市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 在实数0,-π, ,-4中,最小的数是( )A、0 B、-π C、 D、-42. 我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示是( )A、0.675×105 B、67.5×103 C、6.75×104 D、6.75×1053. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )
4. 下列运算正确的是( )
A、a2•a4=a8 B、2a2+a2=3a4 C、a6÷a2=a3 D、(ab2)3=a3b65. 如图,在△ABC中,DE∥BC,若 ,则 等于( )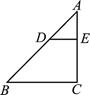 A、
A、 B、
C、
D、
6. “保护水资源,节约用水”应成为每个公民的自觉行为.下表是某个小区随机抽查到的10户家庭的月用水情况,则下列关于这10户家庭的月用水量说法错误的是( )
B、
C、
D、
6. “保护水资源,节约用水”应成为每个公民的自觉行为.下表是某个小区随机抽查到的10户家庭的月用水情况,则下列关于这10户家庭的月用水量说法错误的是( )月用水量(吨)
4
5
6
9
户数(户)
3
4
2
1
A、中位数是5吨 B、众数是5吨 C、极差是3吨 D、平均数是5.3吨7. 若关于x、y的方程组 有实数解,则实数k的取值范围是( )A、k>4 B、k<4 C、k≤4 D、k≥48. 以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )A、b≥1.25 B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤29. 如图,四边形ABCD内接于⊙O,若四边形ABCD是平行四边形,则∠ADC的大小为( )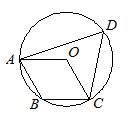 A、 B、
A、 B、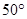 C、
D、
C、
D、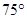 10. 如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )
10. 如图,等边三角形ABC的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A→B→C的方向运动,到达点C时停止.设点M运动的路程为x,MN2=y,则y关于x的函数图象大致为( )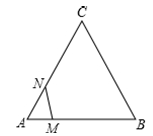 A、
A、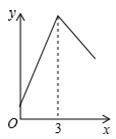 B、
B、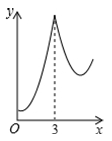 C、
C、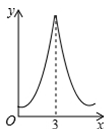 D、
D、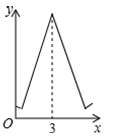
二、填空题
-
11. 若式子 有意义,则实数x的取值范围是 .12. 若点A(3,-4)、B(-2,m)在同一个反比例函数的图象上,则m的值为。13. 有四张质地、大小、反面完全相同的不透明卡片,正面分别写着数字1,2,3,4,现把它们的正面向下,随机摆放在桌面上,从中任意抽出一张,则抽出的数字是奇数的概率是 .14. 如图,已知菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为cm.
 15. 矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为 .
15. 矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为 .三、解答题
-
16. 按要求化简:(a﹣1)÷ ,并选择你喜欢的整数a,b代入求值.
小聪计算这一题的过程如下:
解:原式=(a﹣1)÷ …①
=(a﹣1)• …②
= …③
当a=1,b=1时,原式= …④
以上过程有两处关键性错误,第一次出错在第步(填序号),原因:;
还有第步出错(填序号),原因: .
请你写出此题的正确解答过程.
17. “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图: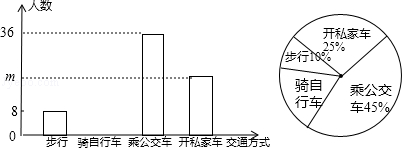 (1)、填空:样本中的总人数为;开私家车的人数m=;扇形统计图中“骑自行车”所在扇形的圆心角为度;(2)、补全条形统计图;(3)、该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?18. 如图,在平行四边形ABCD中,AD>AB.
(1)、填空:样本中的总人数为;开私家车的人数m=;扇形统计图中“骑自行车”所在扇形的圆心角为度;(2)、补全条形统计图;(3)、该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?18. 如图,在平行四边形ABCD中,AD>AB. (1)、作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);(2)、若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.19.
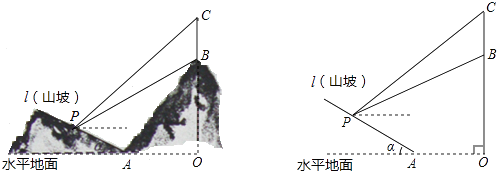
(1)、作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);(2)、若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.19.如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)
 20. 如图1,反比例函数 (x>0)的图象经过点A( ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
20. 如图1,反比例函数 (x>0)的图象经过点A( ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.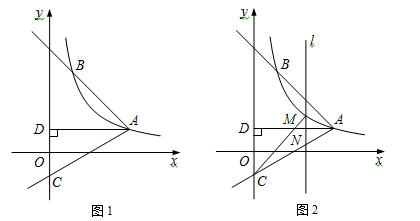 (1)、求k的值;(2)、求tan∠DAC的值及直线AC的解析式;(3)、如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.21. 某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:
(1)、求k的值;(2)、求tan∠DAC的值及直线AC的解析式;(3)、如图2,M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.21. 某品牌手机去年每台的售价y(元)与月份x之间满足函数关系:y=﹣50x+2600,去年的月销量p(万台)与月份x之间成一次函数关系,其中1﹣6月份的销售情况如下表:月份(x)
1月
2月
3月
4月
5月
6月
销售量(p)
3.9万台
4.0万台
4.1万台
4.2万台
4.3万台
4.4万台
(1)、求p关于x的函数关系式;(2)、求该品牌手机在去年哪个月的销售金额最大?最大是多少万元?(3)、今年1月份该品牌手机的售价比去年12月份下降了m%,而销售量也比去年12月份下降了1.5m%.今年2月份,经销商决定对该手机以1月份价格的“八折”销售,这样2月份的销售量比今年1月份增加了1.5万台.若今年2月份这种品牌手机的销售额为6400万元,求m的值.22. 已知AC,EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90.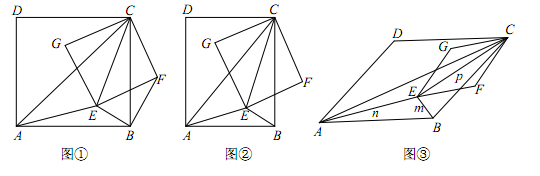 (1)、如图①,当四边形ABCD和EFCG均为正方形时,连接BF.
(1)、如图①,当四边形ABCD和EFCG均为正方形时,连接BF.i)求证:△CAE∽△CBF;
ii)若BE=1,AE=2,求CE的长;
(2)、如图②,当四边形ABCD和EFCG均为矩形,且 时,若BE=1,AE=2,CE=3,求k的值;(3)、如图③,当四边形ABCD和EFCG均为菱形,且∠DAB=∠GEF=45°时,设BE=m,AE=n,CE=p,试探究m,n,p三者之间满足的等量关系.(直接写出结果,不必写出解答过程)23. 如图,已知抛物线经过原点O和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D.直线y=-2x-1经过抛物线上一点B(-2,m)且与y 轴交于点C,与抛物线的对称轴交于点F.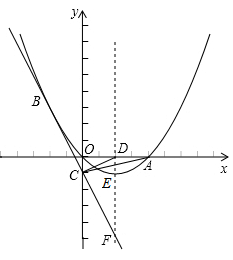
(1)、求抛物线的解析式;(2)、P(x,y)是x轴上方抛物线上的一点,若S△ADP=S△ADC , 求出所有符合条件的点P的坐标;(3)、点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形.若能,请求出点M的运动时间t的值;若不能,请说明理由.