河南省新乡市辉县2018届九年级上学期数学期末考试试卷

试卷更新日期：2019-03-06 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\frac{\sqrt{x - 1}}{x - 2}$ 中x的取值范围是（）

A、x≥1且x≠2 B、x＞1且x≠2 C、x≠2 D、x＞1

查看试题解析
2. 方程x²+6x﹣5＝0的左边配成完全平方后所得方程为（）

A、（x+3）²＝14 B、（x﹣3）²＝14 C、（x+6）²＝ D、以上答案都不对

查看试题解析
3. 已知方程（k﹣3）x²+2x+1＝0有两个实数根，则k的取值范围是（）

A、k＜4 B、k≤4 C、k＜4且k≠3 D、k≤4且k≠3

查看试题解析
4. 如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，则DE的长为（）

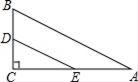A、1 B、2 C、 D、1+

查看试题解析
5. 在平面直角坐标系中，将抛物线y=x²﹣4先向右平移两个单位，再向上平移两个单位，得到的抛物线的解析式是（）

A、y=（x+2）²+2 B、y=（x﹣2）²﹣2 C、y=（x﹣2）²+2 D、y=（x+2）²﹣2

查看试题解析
6. 在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为2：1，把△EFO缩小，则点E的对应点E′的坐标是（）

A、（﹣2，1） B、（﹣8，4） C、（﹣2，1）或（2，﹣1） D、（﹣8，4）或（8，﹣4）

查看试题解析
7. 如图，已知AB是⊙O的直径，∠D＝40°，则∠CAB的度数为（）

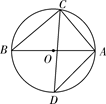A、20° B、40° C、50° D、70°

查看试题解析
8. 下列说法不正确的是（）

A、为了审核书稿中的错别字，选择全面调查 B、为了了解春节联欢晚会的收视率，选择抽样调查 C、“射击运动员射击一次命中靶心”是随机事件 D、“经过由交通信号灯的路口，遇到红灯”是必然事件

查看试题解析
9. 如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，且∠DCE＝∠B．那么下列各判断中，错误的是（）

A、△ADE∽△ABC B、△ADE∽△ACD C、△DEC∽△CDB D、△ADE∽△DCB

查看试题解析
10. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax²+bx+c﹣m＝0有两个不相等的实数根，下列结论：①b²﹣4ac＜0；②abc＞0；③a﹣b+c＜0；④m＞﹣2，其中，正确的个数有（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 3 $\sqrt{18} - \sqrt{2}$ ＝．

查看试题解析
12. ⊙O的直径为8，圆心O到直线l的距离为4，则直线l与⊙O的位置关系是．

查看试题解析
13. 从1，2，3，4这四个数字中，任意抽取两个不同数字组成一个两位数，则这个两位数能被3整除的概率是.

查看试题解析
14. 已知点A（4，y₁），B（2，y₂），C（-2，y₃）都在二次函数y=(x-2)²-1的图象上，则y₁ ， y₂ ， y₃的大小关系是.

查看试题解析
15. 如图，AC⊥BC，AC=BC=4，以AC为直径作半圆，圆心为点O；以点C为圆心，BC为半径作 $\overset{⌢}{A B}$ ．过点O作BC的平行线交两弧于点D、E，则阴影部分的面积是．

查看试题解析

三、解答题

16. 计算：| $\sqrt{2}$ ﹣2|﹣2cos45°+（﹣1）^﹣²+ $\sqrt{8}$ ．

查看试题解析
17. 已知关于x的一元二次方程x²﹣（k+2）x+2k＝0

(1)、求证：无论k取任何实数，方程总有实数根．

(2)、若等腰三角形的一边长为5，另两边长恰好是这个方程的两个根，求这个等腰三角形的周长．

查看试题解析
18. 一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率为 $\frac{1}{2}$ 。

(1)、布袋里红球有多少个？

(2)、先从布袋中摸出1个球后不放回，再摸出1个球，请用列表或画树状图等方法求出两次摸到的球都是白球的概率。

查看试题解析
19. 某公园的人工湖边上有一座假山，假山顶上有一竖起的建筑物CD，高为10米，数学小组为了测量假山的高度DE，在公园找了一水平地面，在A处测得建筑物点D（即山顶）的仰角为35°，沿水平方向前进20米到达B点，测得建筑物顶部C点的仰角为45°，求假山的高度DE．（结果精确到1米，参考数据：sin35°≈ $\frac{7}{12}$ ，cos35°≈ $\frac{5}{6}$ ，tan35°≈ $\frac{7}{10}$ ）

查看试题解析
20. 如图，已知AB是⊙O的直径，过O点作OP⊥AB，交弦AC于点D，交⊙O于点E，且使∠PCA=∠ABC．

(1)、求证：PC是⊙O的切线；

(2)、若∠P=60°，PC=2，求PE的长．

查看试题解析
21. 甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分，如图，甲在O点正上方1m的P处发出一球，羽毛球飞行的高度y（m）与水平距离x（m）之间满足函数表达式y＝a（x﹣4）²+h，已知点O与球网的水平距离为5m，球网的高度为1.55m．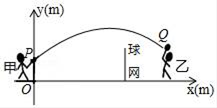

(1)、当a＝﹣ $\frac{1}{24}$ 时，①求h的值；②通过计算判断此球能否过网．

(2)、若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为 $\frac{12}{5}$ m的Q处时，乙扣球成功，求a的值．

查看试题解析
22. 某农场去年种植了10亩地的南瓜，亩产量为2000kg，根据市场需要，今年该农场扩大了种植面积，并且全部种植了高产的新品种南瓜，设南瓜种植面积的增长率为 $x$ .

(1)、则今年南瓜的种植面积为亩；(用含 $x$ 的代数式表示)

(2)、如果今年南瓜亩产量的增长率是种植面积的增长率的 $\frac{1}{2}$ ，今年南瓜的总产量为60000kg，求南瓜亩产量的增长率.

查看试题解析
23. 如图，抛物线y＝﹣ $\frac{1}{2} x^{2}$ +mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．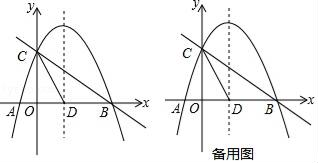

(1)、求抛物线的解析式；

(2)、点E是线段BC上的一个动点（不与B、C重合），过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时点E的坐标．

(3)、在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由．

查看试题解析