河南省洛阳市宜阳县2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 方程2x(x-1)=x-1的解是( )A、x1= ,x2=1 B、x1=- ,x2=1 C、x1=- ,x2=1 D、x1= ,x2=-12. 如果两个相似五边形的面积和等于65cm2 , 其中一组对应边的长分别为3cm和4.5cm,那么较大五边形的面积为( )
A、26cm2 B、39cm2 C、20cm2 D、45cm23. 若一直角三角形两边长分别为12和5,则第三边长为( )A、13 B、13或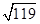 C、13或15
D、15
4. 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,则∠A的正弦值是( )
C、13或15
D、15
4. 在下列网格中,小正方形的边长为1,点A,B,O都在格点上,则∠A的正弦值是( ) A、 B、
A、 B、 C、
C、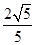 D、
5. 在△ABC中,若AC:BC:AB=7:24:25,则sinA=( )A、
D、
5. 在△ABC中,若AC:BC:AB=7:24:25,则sinA=( )A、 B、
B、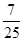 C、
C、 D、
D、 6. 在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是( )A、随着抛掷次数的增加,正面朝上的频率越来越小 B、当抛掷的次数很大时,正面朝上的次数一定占总抛掷次数的 C、不同次数的试验,正面朝上的频率可能会不相同 D、连续抛掷11次硬币都是正面朝上,第12次抛掷出现正面朝上的概率小于7. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、
6. 在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是( )A、随着抛掷次数的增加,正面朝上的频率越来越小 B、当抛掷的次数很大时,正面朝上的次数一定占总抛掷次数的 C、不同次数的试验,正面朝上的频率可能会不相同 D、连续抛掷11次硬币都是正面朝上,第12次抛掷出现正面朝上的概率小于7. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、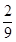 D、
D、 8. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
8. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )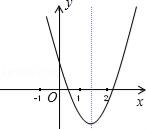 A、1个 B、2个 C、3个 D、4个9. 如图,若△ABC内接于半径为R的⊙O,且∠A=60°,连接OB,OC,则边BC的长为( )
A、1个 B、2个 C、3个 D、4个9. 如图,若△ABC内接于半径为R的⊙O,且∠A=60°,连接OB,OC,则边BC的长为( ) A、 R B、 R C、
A、 R B、 R C、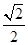 R
D、 R
10. 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P从点A运动到点D时,点Q所经过的路径长为( )
R
D、 R
10. 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点,过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P从点A运动到点D时,点Q所经过的路径长为( ) A、
A、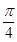 B、
B、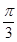 C、
C、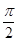 D、π
D、π
二、填空题
-
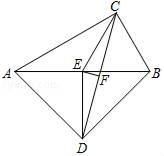
11. 把一副三角板如图放置,E是AB的中点,连接CE、DE、CD,F是CD的中点,连接EF.若AB=8,则S△CEF= .
 12. 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是 .
12. 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是 . 13. 点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1 , y2 , y3的大小关系是 .14. 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .
13. 点A(﹣3,y1),B(2,y2),C(3,y3)在抛物线y=2x2﹣4x+c上,则y1 , y2 , y3的大小关系是 .14. 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .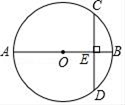 15. 若等边三角形ABC的边长为 cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是 .
15. 若等边三角形ABC的边长为 cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是 .三、解答题
-
16. 在平面直角坐标系中,若△ABC的三个顶点的坐标分别为A(﹣4,1),B(﹣1,3),C(﹣4,3),求sinB的值.
 17. 经过校园某路口的行人,可能左转,也可能直行或右转.假设这三种可能性相同,现有小明和小亮两人经过该路口,请用列表法或画树状图法,求两人之中至少有一人直行的概率.
17. 经过校园某路口的行人,可能左转,也可能直行或右转.假设这三种可能性相同,现有小明和小亮两人经过该路口,请用列表法或画树状图法,求两人之中至少有一人直行的概率.
18. 已知抛物线y=﹣2x2+4x+1.
(1)、求这个抛物线的对称轴和顶点坐标;
(2)、将这个抛物线平移,使顶点移到点P(-2,0)的位置,写出所得新抛物线的表达式和平移的过程.
19. 如图,已知OA、OB、OC是⊙O的三条半径,点C是弧AB的中点,M、N分别是OA、OB的中点.求证:MC=NC. 20. 如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
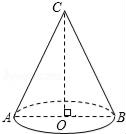
20. 如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE. (1)、试判断∠AED与∠C的数量关系,并说明理由;(2)、若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .21. 小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=3cm,高OC=4cm,这个圆锥漏斗的侧面积是多少?侧面展开图所对的圆心角是多少度?
(1)、试判断∠AED与∠C的数量关系,并说明理由;(2)、若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .21. 小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=3cm,高OC=4cm,这个圆锥漏斗的侧面积是多少?侧面展开图所对的圆心角是多少度?