甘肃省临洮县2019届九年级上学期数学期末考试试卷

试卷更新日期：2019-03-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 把二次函数 $y = 3 x^{2}$ 的图象向左平移2个单位，再向上平移1个单位，所得到的图象对应的二次函数关系式是（）

A、； B、； C、 D、

查看试题解析
3. 随机掷一枚均匀的硬币两次，落地后至少有一次正面朝上的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{3}{4}$ D、1

查看试题解析
4. 若反比例函数 $y = \frac{k - 1}{x}$ 的图象位于第二、四象限，则k的取值可能是（）

A、0 B、2 C、3 D、4

查看试题解析
5. 下列图形中，绕它的中心旋转60°后可以和原图形重合的是（）

A、正六边形 B、正五边形 C、正方形 D、正三角形

查看试题解析
6. 如图，⊙O半径为5，弦AB长为8，M是弦AB上一个动点，则线段OM的最小值为（）

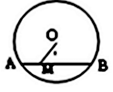A、2 B、3 C、4 D、5

查看试题解析
7. 如图，已知A，B，C均为⊙O上的点，若∠AOB=80°，则∠ACB=（）

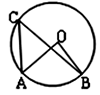A、80° B、70° C、60° D、40°

查看试题解析
8. 如图，点A，B，C，D在⊙O上，若∠B=100°，则∠ADE的度数是（）

A、30° B、50° C、100° D、130°

查看试题解析
9. 如图，从半径为9cm的圆形纸片剪去 $\frac{1}{3}$ 圆周的一个扇形，将留下的扇形围成一个圆锥，那么这个圆锥底面圆的半径为（）

A、6cm B、 cm C、8cm D、 $5 \sqrt{3}$ cm

查看试题解析
10. 若关于 $x$ 的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则 $k$ 的取值范围是（）

A、 B、 C、且 D、且

查看试题解析

二、解答题

11. 解方程：

(1)、 $12 {(x - 2)}^{2} - 9 = 0$

(2)、 $3 {(x - 2)}^{2} = x (x - 2)$

查看试题解析
12. 小明家房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上.

(1)、请帮小明把花坛的位置画出来(尺规作图，不写作法，保留作图痕迹).

(2)、若 $Δ A B C$ 中，AB=8米，AC=6米， $∠ B A C = 90 °$ ，试求小明家圆形花坛的面积.

查看试题解析
13. 圆锥的底面半径为1，母线长为6，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬行一圈再回到点B，问它爬行的最短路线是多少?

查看试题解析
14. 一个不透明的袋子中装有4个完全相同的小球，分别标有数字1、2、3、4，另有一个可以自由转动的转盘．被分成面积相等的3个扇形区，分别标有数字1、2、3（如图所示）．小亮和小丽想通过游戏来决定谁代表学校参加歌咏比赛．游戏规则为：一人从袋子中摸出一个小球，另一个人转动转盘，如果从袋中所摸球上的数字与转盘上转出数字之和小于4，那么小丽去，否则小亮去．

(1)、请用适当的方法求小丽参加比赛的概率；

(2)、你认为该游戏公平吗？请说明理由；若不公平，请修改该游戏规则，使游戏公平．

查看试题解析
15. 如图在坐标系中，直线 $y = x + \frac{1}{2} k$ 与双曲线 $y = \frac{k}{x}$ 在第一象限交于点A，与x轴交于点C，AB垂直x轴，垂足为B，且 $S_{△ A O B} = 1$ .

(1)、求两个函数解析式；

(2)、求△ABC的面积.

查看试题解析
16. 某商店以16元/支的价格进了一批钢笔，如果以20元/支的价格售出，每月可以卖出200支，经市场调查发现，每支钢笔上涨1元，每月就少卖出10支.

(1)、该商店店主希望该笔月销售利润达1350元，则每支钢笔应该上涨多少元？

(2)、每支钢笔上涨多少元时，该商店每月销售利润最大？最大利润是多少？

查看试题解析
17. 如图，在△ABC中，∠C=90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D。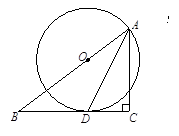

(1)、求证：BC是⊙O切线；

(2)、若BD=5，DC=3，求AC的长。

查看试题解析
18. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交与A(1，0)，B(- 3，0)两点.

(1)、求该抛物线的解析式；

(2)、设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.

(3)、在抛物线上BC段是否存在点P，使得△PBC面积最大，若存在，求P点坐标；若不存在，说明理由.

查看试题解析

三、填空题

19. 已知 $x = - 1$ 是方程 $x^{2} + a x + 3 - a = 0$ 的一个根，则 $a$ 的值是.

查看试题解析
20. 已知点A(m-1，3)与点B(2，n+1)关于 $x$ 轴对称，则点P（m，n）的坐标为．

查看试题解析
21. 如果点（ $a$ ， $- 2 a$ ）在双曲线 $y = \frac{k}{x}$ 上，那么双曲线在第象限．

查看试题解析
22. 李明有红、黑、白3件运动上衣和白、黑2条运动短裤，则穿着“衣裤同色”的概率是．

查看试题解析
23. 已知抛物线 $y = a x^{2} + x + c (a \neq 0)$ 与x轴交于A，B两点．若点A的坐标为(-2，0)，抛物线的对称轴为直线x=2.则线段AB的长为.

查看试题解析
24. 在直角三角形ABC中，∠C=90°，AC=5，BC=12，则这个三角形内切圆的半径是.

查看试题解析
25. 如图，PA、PB、DE分别切⊙O于A、B、C，⊙O的半径长为6cm，PO=10cm，则△PDE的周长是cm．

查看试题解析
26. 如图为二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象，下列说法正确的有.
① $a b c > 0$ ；② $a + b + c > 0$ ；③ $b^{2} - 4 a c < 0$ ④当 $x > 1$ 时，y随x的增大而增大；⑤方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的根是 $x_{1} = - 1$ ， $x_{2} = 3$ .

查看试题解析