甘肃省兰州市2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 方程是关于x的一元二次方程的是( )A、
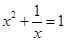 B、
C、
B、
C、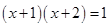 D、
D、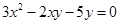 2. 双曲线 经过点 ,则它不经过的点是( )A、(b, a) B、(-a, -b) C、(2a, b/2) D、(-b, a)3. 如图所示几何体,它的俯视图是( )
2. 双曲线 经过点 ,则它不经过的点是( )A、(b, a) B、(-a, -b) C、(2a, b/2) D、(-b, a)3. 如图所示几何体,它的俯视图是( )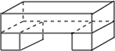 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列说法正确的有( )
4. 下列说法正确的有( )一组对边相等的四边形是矩形; 两条对角线相等的四边形是矩形; 四条边都相等且对角线互相垂直的四边形是正方形; 四条边都相等的四边形是菱形.
A、1 B、2 C、3 D、45. 如图,菱形ABCD的周长为16,∠ABC=120°,则AC的长为( )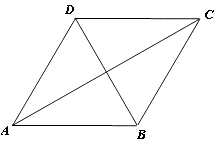 A、 B、4 C、 D、26. 如图, 是菱形 的边 上一点,射线 交 延长线于点 ,则下列比例式中正确的是( )
A、 B、4 C、 D、26. 如图, 是菱形 的边 上一点,射线 交 延长线于点 ,则下列比例式中正确的是( )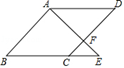 A、
A、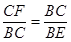 B、
B、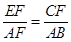 C、
C、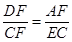 D、
D、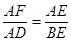 7. 已知 是关于 的方程 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形 的两条边长,则 的周长为( )A、6 B、8 C、10 D、8或108. 已知反比例函数 y= (k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx﹣k的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限9. 一司机驾驶汽车从甲地去乙地,他以 千米/时的平均速度用了 小时到达目的地,当他按原路匀速返回时,汽车的速度 (千米/时)与时间 (小时)的函数关系为( )A、
7. 已知 是关于 的方程 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形 的两条边长,则 的周长为( )A、6 B、8 C、10 D、8或108. 已知反比例函数 y= (k≠0),当x>0时,y随x的增大而增大,那么一次函数y=kx﹣k的图象经过( )A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限9. 一司机驾驶汽车从甲地去乙地,他以 千米/时的平均速度用了 小时到达目的地,当他按原路匀速返回时,汽车的速度 (千米/时)与时间 (小时)的函数关系为( )A、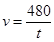 B、
B、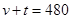 C、
C、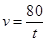 D、
D、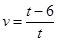 10. 若m,n是一元二次方程x2﹣2x﹣1=0的两个不同实数根,则代数式m2﹣m+n的值是( )A、﹣1 B、3 C、﹣3 D、111. 如图,在直角坐标系中,正方形的中心在原点 ,且正方形的一组对边与 轴平行,点 是反比例函数 的图象上与正方形的一个交点,若图中阴影部分的面积等于 ,则 的值为( )
10. 若m,n是一元二次方程x2﹣2x﹣1=0的两个不同实数根,则代数式m2﹣m+n的值是( )A、﹣1 B、3 C、﹣3 D、111. 如图,在直角坐标系中,正方形的中心在原点 ,且正方形的一组对边与 轴平行,点 是反比例函数 的图象上与正方形的一个交点,若图中阴影部分的面积等于 ,则 的值为( )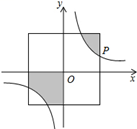 A、16 B、1 C、4 D、-16
A、16 B、1 C、4 D、-16二、解答题
-
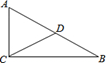
12. 一个口袋装有一双白色和一双黑色手套,两双手套除颜色外其它都相同,现随机从口袋中摸出两只手套,恰好是同颜色的概率是( )A、 B、 C、 D、13. 如图, 中, , , , 是 边的中点, 是 边上一动点(点 不与 、 重合),若以 、 、 为顶点的三角形与 相似,则线段 .
 14. 解关于 的方程.(1)、(2)、(配方法)15. 已知 和 中,有 ,且 和 的周长之差为15厘米,求 和 的周长.16. 关于x的一元二次方程 有实根.(1)、求k的最大整数值;(2)、当k取最大整数值时,方程的根满足 ,求m的值.17. 如图,图中的小方格都是边长为1的正方形, 与 是关于点 为位似中心的位似图形,它们的顶点都在小正方形的顶点上。
14. 解关于 的方程.(1)、(2)、(配方法)15. 已知 和 中,有 ,且 和 的周长之差为15厘米,求 和 的周长.16. 关于x的一元二次方程 有实根.(1)、求k的最大整数值;(2)、当k取最大整数值时,方程的根满足 ,求m的值.17. 如图,图中的小方格都是边长为1的正方形, 与 是关于点 为位似中心的位似图形,它们的顶点都在小正方形的顶点上。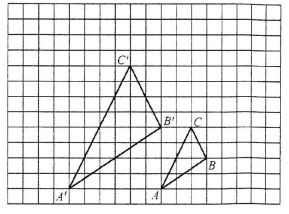 (1)、在图中画出位似中心点 , 与 的相似比是;(2)、以点 为位似中心,再画一个 ,使它与 的相似比等于18. 如图,点 在反比例函数 的图象在第二象限内的分支上, 轴于点 , 是原点,且 的面积为 .试解答下列问题:
(1)、在图中画出位似中心点 , 与 的相似比是;(2)、以点 为位似中心,再画一个 ,使它与 的相似比等于18. 如图,点 在反比例函数 的图象在第二象限内的分支上, 轴于点 , 是原点,且 的面积为 .试解答下列问题: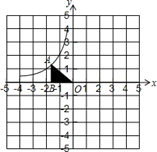 (1)、比例系数 ;(2)、在给定直角坐标系中,画出这个函数图象的另一个分支;(3)、当 时,写出 的取值范围.19. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=__m.
(1)、比例系数 ;(2)、在给定直角坐标系中,画出这个函数图象的另一个分支;(3)、当 时,写出 的取值范围.19. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=__m.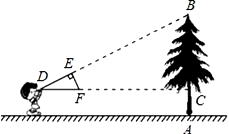 20. 一个不透明的口袋中装有 个分别标有数字 , , , 的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为 ;小颖在剩下的 个小球中随机摸出一个小球记下数字为 .(1)、请用列表法或画树状图的方法表示出由 , 确定的点 所有可能的结果;(2)、小红摸出标有数字 的小球的概率是多少?(3)、若规定:点 在第一象限或第三象限小红获胜;点 在第二象限或第四象限则小颖获胜.请问这个游戏公平吗?21. 在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.(1)、求每张门票的原定票价;(2)、由实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.22. 如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E.
20. 一个不透明的口袋中装有 个分别标有数字 , , , 的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为 ;小颖在剩下的 个小球中随机摸出一个小球记下数字为 .(1)、请用列表法或画树状图的方法表示出由 , 确定的点 所有可能的结果;(2)、小红摸出标有数字 的小球的概率是多少?(3)、若规定:点 在第一象限或第三象限小红获胜;点 在第二象限或第四象限则小颖获胜.请问这个游戏公平吗?21. 在某市组织的大型商业演出活动中,对团体购买门票实行优惠,决定在原定票价基础上每张降价80元,这样按原定票价需花费6000元购买的门票张数,现在只花费了4800元.(1)、求每张门票的原定票价;(2)、由实际情况,活动组织单位决定对于个人购票也采取优惠政策,原定票价经过连续二次降价后降为324元,求平均每次降价的百分率.22. 如图,在矩形ABCD中,AB=4,BC=6,M是BC的中点,DE⊥AM于点E. (1)、求证:△ADE∽△MAB;(2)、求DE的长.23. 如图,已知菱形 ABCD 中,对角线 ACBD 相交于点 O,过点 C 作 CE∥BD,过点 D 作 DE∥AC,CE 与 DE 相交于点 E.
(1)、求证:△ADE∽△MAB;(2)、求DE的长.23. 如图,已知菱形 ABCD 中,对角线 ACBD 相交于点 O,过点 C 作 CE∥BD,过点 D 作 DE∥AC,CE 与 DE 相交于点 E. (1)、求证:四边形 CODE 是矩形.(2)、若 AB=5,AC=6,求四边形 CODE 的周长.24. 已知反比例函数 的图象经过点 .(1)、试确定此反比例函数的解析式;(2)、点 是坐标原点,将线段 绕 点顺时针旋转 得到线段 .判断点 是否在此反比例函数的图象上,并说明理由;(3)、已知点 也在此反比例函数的图象上(其中 ),过 点作 轴的垂线,交 轴于点 .若线段 上存在一点 ,使得 的面积是 ,设 点的纵坐标为 ,求 的值.
(1)、求证:四边形 CODE 是矩形.(2)、若 AB=5,AC=6,求四边形 CODE 的周长.24. 已知反比例函数 的图象经过点 .(1)、试确定此反比例函数的解析式;(2)、点 是坐标原点,将线段 绕 点顺时针旋转 得到线段 .判断点 是否在此反比例函数的图象上,并说明理由;(3)、已知点 也在此反比例函数的图象上(其中 ),过 点作 轴的垂线,交 轴于点 .若线段 上存在一点 ,使得 的面积是 ,设 点的纵坐标为 ,求 的值.三、填空题