江苏省响水县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 下面图形分别表示低碳、节水、节能和绿色食品四个标志,其中的轴对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 点P( 2,-3 )关于x轴的对称点是( )
2. 点P( 2,-3 )关于x轴的对称点是( )
A、(-2, 3 ) B、(2,3) C、(-2,-3 ) D、(2,-3 )3. 若分式 有意义,则实数 的取值范围是( )A、 =3
B、
=3
B、 =0
C、
=0
C、 ≠3
D、
≠3
D、 ≠0
4. 9的算术平方根是( )A、 3 B、-3 C、±3 D、5. 直角三角形中,有两条边长分别为3和4,则第三条边长是( )A、1 B、5 C、
≠0
4. 9的算术平方根是( )A、 3 B、-3 C、±3 D、5. 直角三角形中,有两条边长分别为3和4,则第三条边长是( )A、1 B、5 C、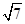 D、5或
D、5或 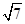 6. 下列图像中,能反映等腰三角形顶角 (度)与底角 (度)之间的函数关系的是( )A、
6. 下列图像中,能反映等腰三角形顶角 (度)与底角 (度)之间的函数关系的是( )A、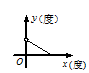 B、
B、 C、
C、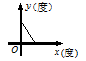 D、
D、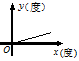
二、填空题
-
7. 在平面直角坐标系中,点A(-5,4)在第象限.8. 分式 、 的最简公分母是 .9. 如果函数y=x-b(b为常数)与函数y=-2x+4的图像的交点坐标是(2,0),那么关于x、y的二元一次方程组 的解是 .10. 如图,△ABC中,DE是边BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=10,则△ABD的周长是 .
 11. 一次函数 = 的图像经过第一、二、四象限,则 的取值范围是 .12. 如图,函数y=2x和y=ax+4的图象相交于点A(1,m),则不等式2x<ax+4的解集为 .
11. 一次函数 = 的图像经过第一、二、四象限,则 的取值范围是 .12. 如图,函数y=2x和y=ax+4的图象相交于点A(1,m),则不等式2x<ax+4的解集为 . 13. 我市市域面积约为16972平方公里,数据16972用四舍五入法精确到千位,并用科学记数法表示为 .14. 如图,Rt△ABC中,∠ACB=90°,D为AB上的点,BD=CD=5,则AD= .
13. 我市市域面积约为16972平方公里,数据16972用四舍五入法精确到千位,并用科学记数法表示为 .14. 如图,Rt△ABC中,∠ACB=90°,D为AB上的点,BD=CD=5,则AD= . 15. 已知关于 的分式方程 = ,若采用乘以最简公分母的方法解此方程,会产生增根,则 的值是 .16. 已知直线 = 与坐标轴相交于A、B两点,动点P从原点O出发,以每秒1个单位长度的速度沿 轴正方向运动,当点P的运动时间是秒时,△PAB是等腰三角形.
15. 已知关于 的分式方程 = ,若采用乘以最简公分母的方法解此方程,会产生增根,则 的值是 .16. 已知直线 = 与坐标轴相交于A、B两点,动点P从原点O出发,以每秒1个单位长度的速度沿 轴正方向运动,当点P的运动时间是秒时,△PAB是等腰三角形.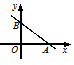
三、解答题
-
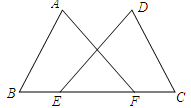
17. 计算:(1)、 ;(2)、 .18. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
 19. 解方程:(1)、 =4;(2)、 = .20. 如图,要在公园(四边形ABCD)中建造一座音乐喷泉(记为点P),使喷泉P到公园两个出入口A、C的距离相等,且到公园的围墙AB、BC的距离相等.请用尺规作图的方法确定喷泉的位置P.(不写作法,保留作图痕迹)
19. 解方程:(1)、 =4;(2)、 = .20. 如图,要在公园(四边形ABCD)中建造一座音乐喷泉(记为点P),使喷泉P到公园两个出入口A、C的距离相等,且到公园的围墙AB、BC的距离相等.请用尺规作图的方法确定喷泉的位置P.(不写作法,保留作图痕迹)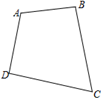 21. 如图,数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子拉直垂到了地面还多1米,同学们把绳子的末端拉开5米后,发现绳子末端刚好接触地面,求旗杆的高度.(旗杆顶端滑轮上方的部分忽略不计)
21. 如图,数学活动课上,老师组织学生测量学校旗杆的高度,同学们发现系在旗杆顶端的绳子拉直垂到了地面还多1米,同学们把绳子的末端拉开5米后,发现绳子末端刚好接触地面,求旗杆的高度.(旗杆顶端滑轮上方的部分忽略不计)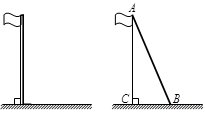 22. 如图,一次函数 = 的图像与正比例函数 = 的图像相交于点A(2, ),与 轴相交于点B.
22. 如图,一次函数 = 的图像与正比例函数 = 的图像相交于点A(2, ),与 轴相交于点B. (1)、求 、 的值;(2)、在 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.23. 如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.
(1)、求 、 的值;(2)、在 轴上存在点C,使得△AOC的面积等于△AOB的面积,求点C的坐标.23. 如图1,在四边形ABCD中,DC∥AB,BD平分∠ABC,CD=4.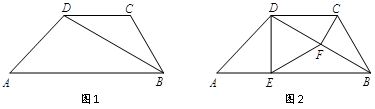 (1)、求BC的长;(2)、如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.24. 张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为 (千克),在甲园所需总费用为 (元),在乙园所需总费用为 (元), 、 与 之间的函数关系如图所示,折线OAB表示 与 之间的函数关系.
(1)、求BC的长;(2)、如图2,若∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.请判断△DEF的形状并证明你的结论.24. 张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为 (千克),在甲园所需总费用为 (元),在乙园所需总费用为 (元), 、 与 之间的函数关系如图所示,折线OAB表示 与 之间的函数关系. (1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克元;(2)、当 >10时,求 与 的函数表达式;(3)、游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.25. 图书管理员小张要骑车从学校到教育局,一出校门,遇到了王老师,王老师说:“今天有风,而且去时逆风,要吃亏了”,小张回答说:“去时逆风,回来时顺风,和无风往返一趟所用时间相同”.(顺风速度=无风时骑车速度+风速,逆风速度=无风时骑车速度-风速)(1)、如果学校到教育局的路程是15 km,无风时小张骑自行车的速度是20 km/h,他逆风去教育局所用时间是顺风回学校所用时间的 倍,求风速是多少?(2)、如果设从学校到教育局的路程为s千米,无风时骑车速度为v千米/时,风速为a千米/时(v>a),那么有风往返一趟的时间无风往返一趟的时间(填“>”、“<”或“=”),试说明理由.26. 截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克元;(2)、当 >10时,求 与 的函数表达式;(3)、游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.25. 图书管理员小张要骑车从学校到教育局,一出校门,遇到了王老师,王老师说:“今天有风,而且去时逆风,要吃亏了”,小张回答说:“去时逆风,回来时顺风,和无风往返一趟所用时间相同”.(顺风速度=无风时骑车速度+风速,逆风速度=无风时骑车速度-风速)(1)、如果学校到教育局的路程是15 km,无风时小张骑自行车的速度是20 km/h,他逆风去教育局所用时间是顺风回学校所用时间的 倍,求风速是多少?(2)、如果设从学校到教育局的路程为s千米,无风时骑车速度为v千米/时,风速为a千米/时(v>a),那么有风往返一趟的时间无风往返一趟的时间(填“>”、“<”或“=”),试说明理由.26. 截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.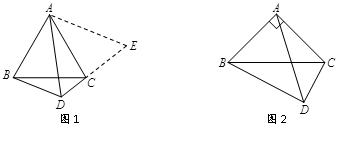 (1)、如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
(1)、如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)
(2)、如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.