甘肃省临洮县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-03-06 类型:期末考试
一、单选题
-
1. 第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部分图形,其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 某种计算机完成一种疾病运算所需的时间约为0.0000000003秒,试用科学记数法表示该数( )A、
2. 某种计算机完成一种疾病运算所需的时间约为0.0000000003秒,试用科学记数法表示该数( )A、 B、
B、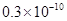 C、
C、 D、
D、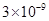 3. 三角形三条高的交点一定在( )A、三角形的内部 B、三角形的外部 C、三角形的内部或外部 D、三角形的内部、外部或顶点4. 在式子 , , , , , 中,分式的个数是 ( )A、2 B、3 C、4 D、55. 等腰三角形的一个内角是50°,则另外两个角的度数分别是( )A、65°,65° B、50°,80° C、65°,65°或50°,80° D、50°,50°6. 若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形7. 下列式子正确的是( )A、
3. 三角形三条高的交点一定在( )A、三角形的内部 B、三角形的外部 C、三角形的内部或外部 D、三角形的内部、外部或顶点4. 在式子 , , , , , 中,分式的个数是 ( )A、2 B、3 C、4 D、55. 等腰三角形的一个内角是50°,则另外两个角的度数分别是( )A、65°,65° B、50°,80° C、65°,65°或50°,80° D、50°,50°6. 若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形7. 下列式子正确的是( )A、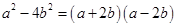 B、
B、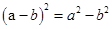 C、
C、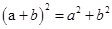 D、
D、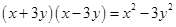 8. 若把分式 中的x,y同时扩大2倍,则分式的值( )A、扩大2倍 B、缩小2倍 C、不变 D、无法确定9. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )A、
8. 若把分式 中的x,y同时扩大2倍,则分式的值( )A、扩大2倍 B、缩小2倍 C、不变 D、无法确定9. 某厂接到加工720件衣服的订单,预计每天做48件,正好按时完成,后因客户要求提前5天交货,设每天应多做x件,则x应满足的方程为( )A、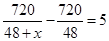 B、
B、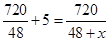 C、
C、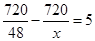 D、
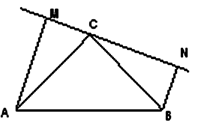
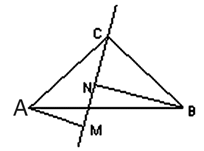
D、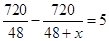 10. 如图,用尺规作图作一个角等于已知角,则说明 =∠AOB的依据是( )
10. 如图,用尺规作图作一个角等于已知角,则说明 =∠AOB的依据是( )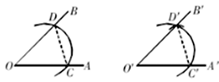 A、SSS B、SAS C、ASA D、AAS
A、SSS B、SAS C、ASA D、AAS二、填空题
-
11. 分解因式: =.12. 计算: =.13. 如图,C、D点在BE上,∠1=∠2,BD=EC,请补充一个条件: , 使△ABC≌△FED.

14. 是完全平方式,则 .15. 计算: =.16. 如图,在Rt△ABC中,∠ACB=90°,AB边的垂直平分线交AB于点E,交BC于点D,且∠ADC=30°,BD=18cm,则AC的长度是cm.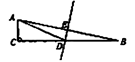 17.
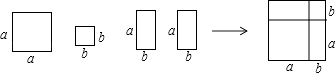
17.利用1个a×a的正方形,1个b×b的正方形和2个a×b的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式 .
 18. 古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为 ,第二个三角形数记为 ,…第n个三角形数记为 ,其中 , , ,…,则 =.
18. 古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,它有一定的规律性,若把第一个三角形数记为 ,第二个三角形数记为 ,…第n个三角形数记为 ,其中 , , ,…,则 =.三、解答题
-
19. 如图,在平面直角坐标系中,A(1, 2),B(3, 1),C(-2, -1).
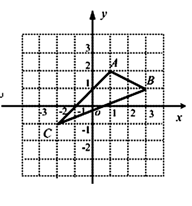 (1)、在图中作出 关于 轴对称的 .(2)、写出点 的坐标(直接写答案).
(1)、在图中作出 关于 轴对称的 .(2)、写出点 的坐标(直接写答案).A1 , B1 , C1 ;
(3)、求△ABC的面积.20. 计算21. 计算(1)、 ;(2)、22.(1)、因式分解:(2)、解分式方程:23. 如图,点B、E、C、F在同一直线上,∠A=∠D,AB∥DE,BE=CF.求证:AC=DF. 24. 先化简,再求值: ,其中x=0.
24. 先化简,再求值: ,其中x=0.