浙教版2019中考数学复习专题之一次函数综合与应用-在线组卷题库

1. 已知直线L₁的解析式为y＝﹣3x+3，L₁与x轴交于点D，直线L₂的解析式为y＝

\frac{3}{2}

x+k，且直线L₁与直线L₂交于点C（2，m），直线L₂与x轴交于点A．

(1)、求k，m的值；

(2)、求△ADC的面积；

(3)、在直线L₂上是否存在一点P，使△ADP的面积等于△ADC的面积，若存在求出点P的坐标，若不存在请说明理由．

查看试题解析

2. 如图1，一次函数y＝

\frac{1}{2}

x+4与x轴、y轴分别交于A，B两点．P是x轴上的动点，设点P的横坐标为n．

(1)、当△BPO∽△ABO时，求点P的坐标；

(2)、如图2，过点P的直线y＝2x+b与直线AB相交于C，求当△PAC的面积为20时，点P的坐标；

(3)、如图3，直接写出当以A，B，P为顶点的三角形为等腰三角形时，点P的坐标．

查看试题解析

3. 如图，一次函数y＝﹣

\frac{3}{4}

x+6的图象分别y轴、x轴交于点A、B，点P从点B出发，沿射线BA以每秒1个单位的速度出发，设点P的运动时间为t秒．

(1)、点P在运动过程中，若某一时刻，△OPA的面积为6，求此时P的坐标；

(2)、在整个运动过程中，当t为何值时，△AOP为等腰三角形？（只需写出t的值，无需解答过程）

(3)、若第二象限有一点C（﹣1，4），试问在y轴上是否存在一点M，使BM﹣CM的值最大？如果存在，求出点M的坐标；如果不存在，请说明理由．

查看试题解析

4. 如图，直线y＝

\frac{3}{4}

x+b（b＞0）与x轴、y轴交于点A、B，在直线AB上取一点C，过点C作x轴的垂线，垂足为E，若点E（4，0）．

(1)、若EC＝BC，求b的值；

(2)、在（1）的条件下，有一动点P从点B出发，延着射线BC方向以每秒1个单位的速度运动，以点P为圆心，作半径为

\frac{1}{2}

的圆，动点Q从点O出发，在线段OE上以每秒1个单位的速度作来回运动，过点Q作直线l垂直x轴，点P与点Q同时从点B、点O开始运动，问经过多少秒后，直线l和⊙P相切．

查看试题解析

5. 如图①，在平面直角坐标系中，直线y＝kx+b与x轴正半轴交于点A，与y轴负半轴交于点B，圆心P在x轴的正半轴上，已知AB＝10，AP＝

\frac{25}{4}

(1)、求点P到直线AB的距离；

(2)、求直线y＝kx+b的解析式；

(3)、在图②中存在点Q，使得∠BQO＝90°，连接AQ，请求出AQ的最小值．

查看试题解析

6. 张庄甲、乙两家草莓采摘园的草莓销售价格相同，“春节期间”，两家采摘园将推出优惠方案，甲园的优惠方案是：游客进园需购买门票，采摘的草莓六折优惠；乙园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，某游客的草莓采摘量为x（千克），在甲园所需总费用为y_甲（元），在乙园所需总费用为y_乙（元），y_甲、y_乙与x之间的函数关系如图所示，折线OAB表示y_乙与x之间的函数关系．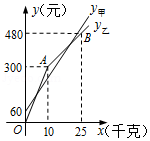

(1)、甲采摘园的门票是元，两个采摘园优惠前的草莓单价是每千克元；

(2)、当x＞10时，求y_乙与x的函数表达式；

(3)、游客在“春节期间”采摘多少千克草莓时，甲、乙两家采摘园的总费用相同．

查看试题解析

7. A市和B市分别有某种库存机器12台和6台，现决定支援C村10台，D村8台，已知从A市调运一台机器到C村和D村的运费分别是400元和800元，从B市调运一台机器到C村和D村的运费分别是300元和500元．

(1)、设B市运往C村机器x台，求总运费W关于x的函数关系式；

(2)、若要求总运费不超过9200元，共有几种调运方案？

(3)、写出总运费最低的调运方案，最低运费是多少元？

查看试题解析

8. 目前节能灯在城市已基本普及，今年安徽省面向县级及农村地区推广，为响应号召，某商场计划购进甲、乙两种节能灯共1200只，这两种节能灯的进价、售价如下表：

	进价（元/只）	售价（元/只）
甲型	25	30
乙型	45	60

(1)、如何进货，进货款恰好为46000元？

(2)、设商场购进甲种节能灯x只，求出商场销售完节能灯时总利润w与购进甲种节能灯x之间的函数关系式．

(3)、如何进货，商场销售完节能灯时获利13500元

查看试题解析

9. 某农庄计划在30亩空地上全部种植蔬菜和水果，菜农小张和果农小李分别承包了种植蔬菜和水果的任务．小张种植每亩蔬菜的工资y（元）与种植面积m（亩）之间的函数关系如图①所示，小李种植水果所得报酬z（元）与种植面积n（亩）之间的函数关系如图②所示．

(1)、如果种植蔬菜20亩，则小张种植每亩蔬菜的工资是元，小张应得的工资总额是元，此时，小李种植水果亩，小李应得的报酬是元；

(2)、当10＜n≤30时，求z与n之间的函数关系式；

(3)、设农庄支付给小张和小李的总费用为W（元），当10＜m≤30时，求W与m之间的函数关系式，并求出总费用最大为多少？

查看试题解析

10. 随着地球上的水资源日益枯竭，各级政府越来越重视节约用水．某市民生活用水按“阶梯水价”方式进行收费，人均月生活用水收费标准如图所示，图中x表示人均月生活用水的吨数，y表示收取的人均月生活用水费（元）．请根据图象信息，回答下列问题：

(1)、该市人均月生活用水的收费标准是：不超过5吨，每吨按元收取；超过5吨的部分，每吨按元收取；

(2)、当x＞5时，求y与x的函数关系式；

(3)、若某个家庭有5人，五月份的生活用水费共76元，则该家庭这个月用了多少吨生活用水？

查看试题解析

11. 如图，直线y＝﹣

\frac{1}{2}

x+3与x轴、y轴分别相交于A，B两点，P是线段AB上的一个动点（不与AB两点重合），点M的坐标为（4，0），设P点的横坐标为x，设△OPM的面积为S．

(1)、求点A，B的坐标；

(2)、求S关于x的函数解析式，并写出自变量x的取值范围；

(3)、当S＝

\frac{1}{2}

S_△AOB时，求点P的坐标；

(4)、画出函数S的图象．

查看试题解析

12. 如图，直线y₁＝﹣2x+3与直线y₂＝﹣x+9相交于点A，且与x轴y轴分别交于点B，C，点P是x轴上的动点．

(1)、求点A坐标；

(2)、当PA+PC的值最小时，求此时点P的坐标；

(3)、在（2）条件下，若点E的坐标为（a，2a²﹣1），点F在直线y₁＝ax+a上，且四边形ECFP是平行四边形，求出a的值．

查看试题解析

13. 如图

材料一：如图1，由课本91页例2画函数y＝﹣6x与y＝﹣6x+5可知，直线y＝﹣6x+5可以由直线y＝﹣6x向上平移5个单位长度得到由此我们得到正确的结论一：

在直线l₁：y＝k₁x+b₁与直线l₂：y＝k₂x+b₂中，如果k₁＝k₂且b₁≠b₂ ，那么l₁∥l₂ ，反过来，也成立．

材料二：如图2，由课本92页例3画函数y＝2x﹣1与y＝﹣0.5x+1可知，利用所学知识一定能证出这两条直线是互相垂直的．由此我们得到正确的结论二：

在直线l₁：y＝k₁x+b₁与l₂：y＝k₂x+b₂中，如果k₁•k₂＝﹣1，那么l₁⊥l₂ ，反过来，也成立

应用举例

已知直线y＝﹣ $\frac{1}{6}$ x+5与直线y＝kx+2互相垂直，则﹣ $\frac{1}{6}$ k＝﹣1．所以k＝6

解决问题

(1)、请写出一条直线解析式，使它与直线y＝x﹣3平行．

(2)、如图3，点A坐标为（﹣1，0），点P是直线y＝﹣3x+2上一动点，当点P运动到何位置时，线段PA的长度最小？画出图形（保留画图痕迹，不写画法）并求出此时点P的坐标．

查看试题解析

14. 定义：斜率表示一条直线y＝kx+b（k≠0）关于橫坐标轴倾斜程度的量，即直线与x轴正方向夹角（倾斜角α）的正切值，表示成k＝tanα．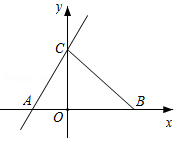

(1)、直线y＝x﹣2b的倾斜角α＝．

(2)、如图，在△ABC中，tanA、tanB是方程x²﹣（

\sqrt{3}

+1）x+

\sqrt{3}

＝0的两根，且∠A＞∠B，B点坐标为（5，0），求出直线AC关系式．

查看试题解析

15. 如图，在平面直角坐标系中，直线l₁的解析式为y＝﹣x，直线l₂与l₁交于点A（a，﹣a），与y轴交于点B（0，b），其中a，b满足（a+3）²+

\sqrt{b - 4}

＝0．

(1)、求直线l₂的解析式；

(2)、在平面直角坐标系中第二象限有一点P（m，5），使得S_△AOP＝S_△AOB ，请求出点P的坐标；

(3)、已知平行于y轴左侧有一动直线，分别与l₁ ， l₂交于点M、N，且点M在点N的下方，点Q为y轴上一动点，且△MNQ为等腰直角三角形，请求出满足条件的点Q的坐标．

查看试题解析

16. 在平面直角坐标系xOy中，直线l₁：y＝

\frac{1}{2}

x+b与x轴交于点A，与y轴交于点B，且点C的坐标为（4，﹣4）．

(1)、点A的坐标为，点B的坐标为；（用含b的式子表示）

(2)、当b＝4时，如图所示．连接AC，BC，判断△ABC的形状，并证明你的结论；

(3)、过点C作平行于y轴的直线l₂ ，点P在直线l₂上．当﹣5＜b＜4时，在直线l₁平移的过程中，若存在点P使得△ABP是以AB为直角边的等腰直角三角形，请直接写出所有满足条件的点P的纵坐标．

查看试题解析

17. 如图，在平面直角坐标系中，直线l₁：y＝﹣

\frac{1}{2}

x+6分别与x轴、y轴交于点B、C，且与直线l₂：y＝

\frac{1}{2}

x交于点A．

(1)、点A的坐标是；点B的坐标是；点C的坐标是；

(2)、若D是线段OA上的点，且△COD的面积为12，求直线CD的函数表达式；

(3)、在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析

18. 如图，直线l₁：y₁＝﹣x+2与x轴，y轴分别交于A，B两点，点P（m，3）为直线l₁上一点，另一直线l₂：y₂＝

\frac{1}{2}

x+b过点P．

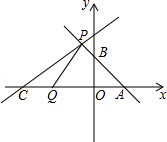(1)、求点P坐标和b的值；

(2)、若点C是直线l₂与x轴的交点，动点Q从点C开始以每秒1个单位的速度向x轴正方向移动．设点Q的运动时间为t秒．

①请写出当点Q在运动过程中，△APQ的面积S与t的函数关系式；

②求出t为多少时，△APQ的面积小于3；

③是否存在t的值，使△APQ为等腰三角形？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析

19. 已知直线

y = \frac{1}{2} x + b

与x轴交于点A（﹣4，0），与y轴交于点B．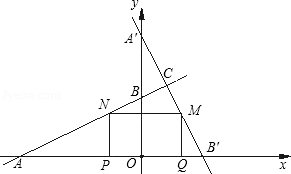

(1)、求b的值；

(2)、把△AOB绕原点O顺时针旋转90°后，点A落在y轴的A′处，点B若在x轴的B′处．

①求直线A′B′的函数关系式；

②设直线AB与直线A′B′交于点C，矩形PQMN是△AB′C的内接矩形，其中点P，Q在线段AB′上，点M在线段B′C上，点N在线段AC上．若矩形PQMN的两条邻边的比为1：2，试求矩形PQMN的周长．

查看试题解析

20. 如图，A，B是分别在x轴上的原点左右侧的点，点P（2，m）在第一象限内，直线PA交y轴于点C（0，2），直线PB交y轴于点D，S_△AOC＝10．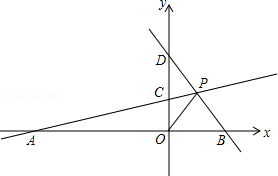

(1)、求点A的坐标及m的值；

(2)、若S_△BOP＝S_△DOP ，求直BD的解析式；

(3)、在（2）的条件下，直线AP上是否存在一点Q，使△QAO的面积等于△BOD面积？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

21. 直线AB：y＝x+b分别与x，y轴交于A，B两点，点A的坐标为（﹣3，0），过点B的直线交x轴正半轴于点C，且OB：OC＝3：1．

(1)、求点B的坐标及直线BC的函数表达式；

(2)、在x轴上方存在点D，使以点A，B，D为顶点的三角形与△ABC全等，画出△ABD，并求出点D的坐标；

(3)、在线段OB上存在点P，使点P到点B，C的距离相等，求出点P的坐标．

查看试题解析

22. 已知一次函数y＝kx+b（k≠0），当x＝3时y＝﹣1，当x＝1时y＝1．

(1)、求该一次函数的表达式；

(2)、请按列表、描点、连线的步骤完成本小题，先补充完整函数值表，然后再在平面直角坐标系中描点，连线作一次函数的图象．

自变量x	…	0		…
函数值y＝kx+b	…		0	…

(3)、该一次函数的图象与x轴，y轴的交点分别是A，B，坐标原点为O，试确定点D，使得它与A，B，O中的两个点作为顶点的三角形与△ABO全等，直接写出满足条件的D点的坐标．

查看试题解析

23. 如图，已知直线l₁：y＝x+2与直线l₂：y＝﹣kx+4（k≠0）相交于点F，直线l₁ ， l₂分别交x轴于点E，G．长方形ABCD的顶点C，D分别在l₂和y轴上，顶点A，B都在x轴上，且点B与点E重合，点A与点O重合，长方形ABCD的面积是12．

(1)、求k的值；

(2)、求证：△EFG是等腰直角三角形；

(3)、若长方形ABCD从原地出发，沿x轴正方向以每秒1个单位长度的速度平移，设移动时间为t秒，长方形ABCD与△EFG重叠部分的面积为S．

①当0≤t≤1时，求S的最大值；

②当1＜t≤4时，直接写出S与t之间的函数关系式（要求写出自变量t的取值范围）．

查看试题解析

24. 孝感市委市政府为了贯彻落实国家的“精准扶贫”战略部署，组织相关企业开展扶贫工作，博大公司为此制定了关于帮扶A、B两贫困村的计划．今年3月份决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗．已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：

目的地

费用

车型

A村（元/辆）

B村（元/辆）

大货车

800

900

小货车

400

600

(1)、求这15辆车中大小货车各多少辆？

(2)、现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总运费为y元；

①试求出y与x的函数解析式；

②若运往A村的鱼苗不少于108箱，请你写出使总运费最少的货车调配方案，并求出最少运费．

查看试题解析

25. 某服装店一次性购进甲、乙两种保暖内衣共100件进行销售，甲、乙两种保暖内衣的进价与售价分别如下表所示：

	甲	乙
进价	80元/件	100元/件
售价	120元/件	150元/件

设购进甲种保暖内衣的数量为x（件）．

(1)、设进货成本为y（元），求y与x之间的函数关系式；

(2)、若除了进货成本以外，从进货到销售完这批内衣的过程中还要支付运费和销售员工工资共200元，设销售完这批保暖内衣的总利润为w（元），请求出w与x之间的函数关系式；

(3)、在（2）的情况下，根据市场需求调研发现，甲种保暖内衣的购进数量不能低于50件，求购进甲种内衣多少件时，这批保暖内衣销售完获利最多？最多可获利多少元？

查看试题解析

26. 某文具店四月份购进甲、乙两种文具共80件，分别用去400元、1200元，甲种文具每件的进价是乙种文具的

\frac{1}{3}

．请解答下列问题：

(1)、求甲、乙两种文具每件的进价；

(2)、五月份文具店决定再次购进甲、乙两种文具共80件，进价不变，甲、乙文具每件售价分别是15元、40元．若80件文具全部售出，求销售甲乙文具获利y（元）与购进甲种文具x（件）之间的函数解析式；

(3)、在（2）的条件下，销售前文具店决定从这80件文具中拿出一部分，赠送给某校在“牡丹江首届汉字听写电视大赛”获一、二等奖的6名同学，作为奖品，其余文具全部售出．已知一等奖每人1件甲种文具，3件乙种文具；二等奖每人4件甲种文具，1件乙种文具，这些奖品总进价超过450元，文具店购进的80件文具仅获利30元．请直接写出文具店购进甲、乙两种文具的方案．

查看试题解析

27. 某学校初二年级在元旦汇演中需要外出租用同一种服装若干件，已知在没有任何优惠的情况下，甲服装店租用2件和在乙服装店租用3件共需280元，在甲服装店租用4件和在乙服装店租用一件共需260元．

(1)、求两个服装店提供的单价分别是多少？

(2)、若该种服装提前一周订货则甲乙两个租售店都可以给予优惠，具体办法如下：甲服装店按原价的八折进行优惠；在乙服装店如果租用5件以上，且超出5件的部分可按原价的六折进行优惠；设需要租用x件服装，选择甲店则需要y₁元，选择乙店则需要y₂元，请分别求出y₁ ， y关于x的函数关系式；

(3)、若租用的服装在5件以上，请问租用多少件时甲乙两店的租金相同？

查看试题解析

28. 为了提高饮水质量，越来越多的居民选购家用净水器．一商场抓住商机，打算从厂家那里购进一批A、B两种型号的家用净水器A型净水器进价是150元/台，B型净水器进价是350元/台，经过协商，厂家给出了两种优惠方案．

第一种优惠方案：A、B两种型号净水器均按进价的8折收费；

第二种优惠方案：A型净水器按原价收费，B型净水器购买数量超过10台后超过部分按6折收费．

该商场只能选择其中一种优惠方案，已知购进A型净水器数量是B型净水器数量的1.5倍．设购进B型净水器x（x＞10）台，第一种优惠方案所需总费用为y₁元，第二种优惠方案所需总费用为y₂元．

(1)、请分别写出y₁ ， y₂与x之间的函数关系式；

(2)、选择哪一种优惠方案花费较少？请说明理由

查看试题解析

29. 某商场筹集资金12.8万元，一次性购进空调，彩电共30台，根据市场需要，这些空调，彩电可以全部销售，全部销售后利润不低于1.5万元，其中空调、彩电的进价和售价如下表所示：

项目	空调	彩电
进价（月/台）	5400	3500
售价（月/台）	6100	3900

设商场计划购进空调x台，空调和彩电全部销售后商场获得的利润为y元．

(1)、试出y与x之间的函数关系式；

(2)、商场有哪几种进货方案可以选择？

(3)、根据你所学的有关函数知识选择哪种方案获利最大，最大利润为多少？

查看试题解析

30. “低碳环保、绿色出行”的理念得到广大群众的接受，越来越多的人喜欢选择自行车作为出行工具．小军和爸爸同时从家骑自行车去图书馆，爸爸先以150米分的速度骑行一段时间，休息了5分钟，再以m米/分的速度到达图书馆．小军始终以同一速度骑行，两人行驶的路程y（米）与时间x（分钟）的关系如图，请结合图象，解答下列问题

(1)、a＝；b＝；m＝．

(2)、若小军的速度是120米/分，求小军在途中与爸爸第二次相遇时，距图书馆的距离；

(3)、在（2）的条件下，爸爸自第二次出发至到达图书馆前何时与小军相距100米？

(4)、若小军的行驶速度是v米/分，且在途中与爸爸恰好相遇两次（不包括家、图书馆两地），请直接写出v的取值范围

查看试题解析

31. 2018年5月，某城遭遇暴雨水灾，武警战士乘一冲锋舟从A地逆流而上，前往C地营救受困群众，途经B地时，由所携带的救生艇将B地受困群众运回A地，冲锋舟继续前进，到C地接到群众后立刻返回A地，途中曾与救生艇相遇，冲锋舟和救生艇距A地的距离y（千米）和冲锋舟出发后所用时间x（分）之间的函数图象如图所示，假设群众上下冲锋舟和救生艇的时间忽略不计，水流速度和冲锋舟在静水中的速度不变．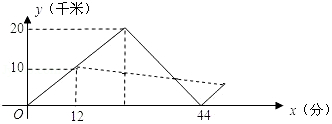

(1)、冲锋舟从A地到C地的时间为分钟，冲锋舟在静水中的速度为千米/分，水流的速度为千米/分．

(2)、冲锋舟将C地群众安全送到A地后，又立即去接应救生艇，已知救生艇与A地的距离y（千米）和冲锋舟出发后所用时间x（分钟）之间的函数关系式为y＝kx+b，若冲锋舟在距离A地

\frac{20}{3}

千米处与救生艇第二次相遇，求k、b的值．

查看试题解析

32. 甲、乙两个仓库要向A、B两地运送水泥，已知甲库可调出水泥100吨，乙库可调出水泥80吨；A地需水泥70吨，B地需水泥110吨，两仓库到A、B两地的路程和运费如下表：

	路程（千米）		运费（元/吨•千米）
	甲库	乙库	甲库	乙库
A地	20	15	12	12
B地	25	20	10	8

(1)、设甲库运往A地水泥x吨，求总运费Y（元）关于x（吨）的函数关系式及x的取值范围；

(2)、当甲、乙两个仓库各运往A、B两地水泥多少吨时总运费最少？最少运费是多少？

查看试题解析

33. “端午节”某顾客到商场购买商品，发现如果购买3件A商品和2件B商品共需花费230元，如果购买4件A商品和1件B商品共需花费240元．

(1)、求A商品、B商品的单价分别是多少元？

(2)、商场在“端午节”开展促销活动，促销方法是：购买A商品超过10件，超过部分可以享受6折优惠，若购买x（x＞0）件A商品需要花费y元，请你求出y与x的函数关系式．

(3)、在（2）的条件下，顾客决定在A、B两种商品中选购其中一种，且数量超过10件，请你帮助顾客判断买哪种商品省钱．

查看试题解析

34. 在学完勾股定理的证明后发现运用“不同方式表示同一图形的面积”可以证明一类含有线段的等式，这种方法称之为面积法．学有所用：在等腰△ABC中，AB＝AC，其一腰上的高为h，M是底边BC上的任意一点，M到腰AB、AC的距离分别为h₁、h₂ ．

(1)、结合图1，（1）结合图1，写出h₁、h₂、h之间有什么样的结论．（不证明）

(2)、如图2，当点M在BC延长线上时，直接写出h₁、h₂、h之间又有什么样的结论；

(3)、利用以上结论解答，如图3在平面直角坐标系中有两条直线l₁：y＝

\frac{3}{4}

x+3，l₂：y＝﹣3x+3，若l₂上的一点M到l₁的距离是

\frac{3}{2}

．求点M的坐标．

查看试题解析

35. 对于点P（x，y），规定x+y＝a，那么就把a叫点P的亲和数．例如：若P（2，3），则2+3＝5，那么5叫P的亲和数．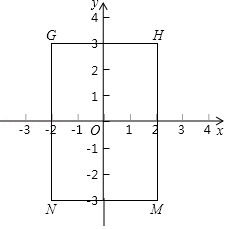

(1)、在平面直角坐标系中，已知，点A（﹣2，6）

①B（1，3），C（3，2），D（2，2），与点A的亲和数相等的点；

②若点E在直线y＝x+6上，且与点A的亲和数相同，则点E的坐标是；

(2)、如图点P是矩形GHMN边上的任意点，且点H（2，3），N（﹣2，﹣3），点Q是直线y＝﹣x+b上的任意点，若存在两点P、Q的亲和数相同，那么求b的取值范围？

查看试题解析

36. 我们对平面直角坐标系xOy中的三角形给出新的定义：三角形的“横长”和三角形的“纵长”．

我们假设点P（x₁ ， y₁），Q（x₂ ， y₂）是三角形边上的任意两点．如果|x₁﹣x₂|的最大值为m，那么三角形的“横长”l_x＝m；如果|y₁﹣y₂|的最大值为n，那么三角形的“纵长”l_y＝n．如图1，该三角形的“横长”l_x＝|3﹣1|＝2；“纵长”l_y＝|3﹣0|＝3．

当l_y＝l_x时，我们管这样的三角形叫做“方三角形”．

(1)、如图2所示，已知点O（0，0），A（2，0）．

①在点C（﹣1，3），D（2，1）， $E (\frac{1}{2} ， - 2)$ 中，可以和点O，点A构成“方三角形”的点是；

(2)、如图3所示，已知点O（0，0），G（1，﹣2），点H为平面直角坐标系中任意一点．若△OGH为“方三角形”，且S_△OGH＝2，请直接写出点H的坐标．

查看试题解析

37. 已知，如图1，直线AB的解析式为y＝x+b，与y轴交于点A，与x轴交于点B，P（m，n）为线段AB上一动点，作PE⊥y轴，PF⊥x轴，垂足分别为E，F，连接EF，PO．

(1)、当b＝5时，则A、B两点的坐标为A（，），B（，）；

(2)、设△PBO的面积为S，在（1）条件下，

①求S关于m的函数关系式；

②是否存在点P使EF最小，若存在，求出EF的最小值并直接写出此时S的值，若不存在，请说明理由；

(3)、如图2另有点M（3，3），连接OM、AM，将△AOM绕点M旋转180°得到△CDM，连接AD，OC，①四边形AOCD的形状是；②若四边形AOCD是正方形，则b＝．

查看试题解析

38. 如图1，直线y＝﹣

\frac{4}{3}

x+8，与x轴、y轴分别交于点A、C，以AC为对角线作矩形OABC，点P、Q分别为射线OC、射线AC上的动点，且有AQ＝2CP，连结PQ，设点P的坐标为P（0，t）．

(1)、求点B的坐标．

(2)、若t＝1时，连接BQ，求△ABQ的面积．

(3)、如图2，以PQ为直径作⊙I，记⊙I与射线AC的另一个交点为E．

①若 $\frac{P E}{P Q}$ ＝ $\frac{3}{5}$ ，求此时t的值．

查看试题解析

39. 阅读材料：

在平面直角坐标系xOy中，点P（x₀ ， y₀）到直线Ax+By+C＝0的距离公式为：d＝ $\frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ．

例如：求点P₀（0，0）到直线4x+3y﹣3＝0的距离．

解：由直线4x+3y﹣3＝0知，A＝4，B＝3，C＝﹣3，

∴点P₀（0，0）到直线4x+3y﹣3＝0的距离为d＝ $\frac{| 4 \times 0 + 3 \times 0 - 3 |}{\sqrt{4^{2} + 3^{2}}}$ ＝ $\frac{3}{5}$ ．

根据以上材料，解决下列问题：

(1)、问题1：点P₁（3，4）到直线y＝﹣

\frac{3}{4}

x+

\frac{5}{4}

的距离为；

(2)、问题2：已知：⊙C是以点C（2，1）为圆心，1为半径的圆，⊙C与直线y＝﹣

\frac{3}{4}

x+b相切，求实数b的值；

(3)、问题3：如图，设点P为问题2中⊙C上的任意一点，点A，B为直线3x+4y+5＝0上的两点，且AB＝2，请求出S_△ABP的最大值和最小值．

查看试题解析

40. 已知直线AB：y=﹣

\frac{1}{2}

x+5与x轴、y轴分别交于点A、B，y轴上点C的坐标为（0，10）．

(1)、求A、B两点的坐标；

(2)、动点M从A点出发，以每秒1个单位长度的速度，沿x轴向左运动，连接CM．设点M的运动时间为t，△COM的面积为S，求S与t的函数关系式；（并标出自变量的取值范围）

(3)、直线AB与直线CM相交于点N，点P为y轴上一点，且始终保持PM+PN最短，当t为何值时，△COM≌△AOB，并求出此时点P的坐标．

查看试题解析

浙教版2019中考数学复习专题之一次函数综合与应用

一、解答题